Giải bài 3 trang 78 toán 7 tập 2 chân trời sáng tạo
Bài 3 trang 78 toán 7 tập 2 CTST
Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng:
a) DE vuông góc với BC.
b) BE vuông góc với DC.
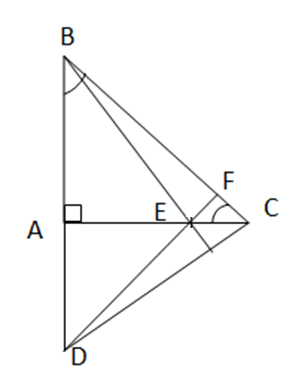
a) Gọi F là giao điểm của DE và BC
+ AD = AE => ∆ADE cân tại A
∆ABC vuông cân tại A => BA ⊥ AC hay EA ⊥ AD
=> ∆ ADE vuông cân tại A
=> $\widehat{AED}$ = $\widehat{ADE}$ = 45°
+ ∆ ABC vuông cân tại A
=> $\widehat{ABC}$ = $\widehat{ACB}$ = 45°
+ Xét ∆EFC có : $\widehat{FEC}$ + $\widehat{FCE}$ + $\widehat{EFC}$ = 180°
=> 45° + 45° + $\widehat{EFC}$ = 180°
=> $\widehat{EFC}$ = 180° - 90° = 90°
=> EF ⊥ BC hay DE ⊥ BC.
b) Xét tam giác BCD có: CA ⊥ BD => CA là đường cao của ∆ BCD
DE ⊥ BC => DE là đường cao của ∆ BCD
Mà DE giao với CA tại E
=> E là trực tâm của ∆ BCD
=> BE ⊥ CD.
Xem toàn bộ: Giải bài 8 Tính chất ba đường cao của tam giác

Bình luận