Giải chi tiết hoạt động khám phá 3 trang 11 chuyên đề toán 12 chân trời sáng tạo

a, Ta có: x ≥ 0; y ≥ 0

Do tiền thu mua không vượt quá 120 triệu đồng nên 12x + 20y ≤ 120 hay 3x + 5y -30 ≤ 0

Do tổng khối lượng trái cây không vượt quá 8 tấn nên x + y ≤ 8 hay x + y – 8 ≤ 0

Lợi nhuận đạt được là P = 1,1x + 1,5y

b, Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

P = 1,1x + 1,5y → max

Với ràng buộc  

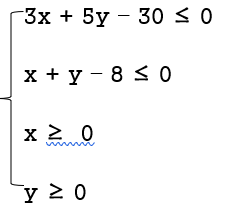
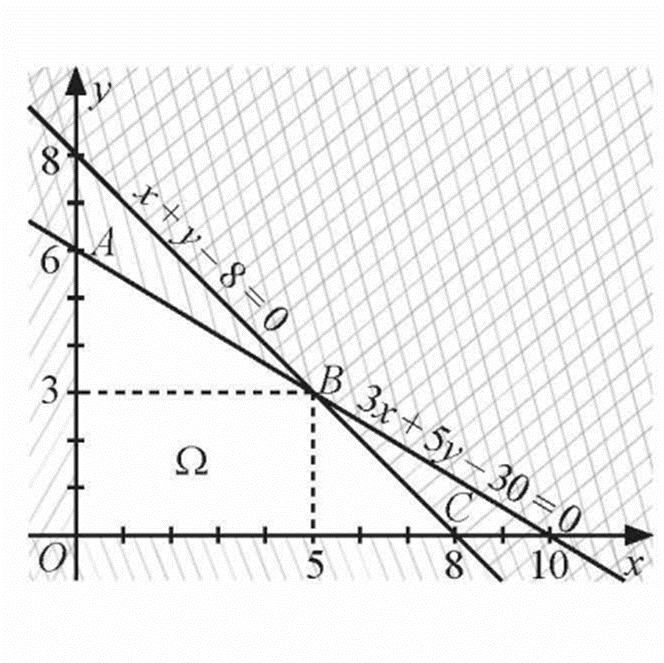
Tập phương án Ω của bài toán là miền tứ giác OABC trong hình trên, trong đó O(0;0), A(0;6), B(5;3), C(8;0)

Giá trị của P tại các đỉnh:

P(0;0) = 1,1.0 + 1,5.0 = 0                             P(0;6) = 1,1.0 + 1,5.6 = 9

P(5;3) = 1,1.5 + 1,5.3 = 10                           P(8;0) = 1,1.8 + 1,5.0 = 8,8

Từ đó P = P(5;3) = 10

Vậy thương nhân đó nên mua 5 tấn trái cây loại A, 3 tấn trái cây loại B để thu được lợi nhuận cao nhất khi bán hết hàng đã mua

Khi đó, lợi nhuận thu được là 10 triệu đồng.