CHƯƠNG V. GIỚI HẠN. HÀM SỐ LIÊN TỤC

BÀI 17: HÀM SỐ LIÊN TỤC

1. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM 

Hoạt động 1. 

Ta có f(1)=2

f(x) =$\frac{x^{2}-1}{x-1}$=$\frac{(x-1)(x+1)}{x-1}$ 

=(x+1) =1+1=2 

Vậy f(x) =f(1).

Khái niệm

Cho hàm số y=f(x) xác định trên khoảng (a;b) chứa điểm x$_{0}$. Hàm số f(x) được gọi là liên tục tại điểm x$_{0}$ nếu f(x) =f(x$_{0}$).

+) Hàm số f(x) không liên tục tị x$_{0}$ được gọi là gián đoạn tại điểm đó.

Ví dụ 1: (SGK – tr.119).

Hướng dẫn giải (SGK – tr.119).

Ví dụ 2: (SGK – tr.120).

Hướng dẫn giải (SGK – tr.120).

Chú ý

Hàm số f(x) liên tục tại x$_{0}$ khi và chỉ khi:

f(x) =f(x) =f(x$_{0}$)

Luyện tập 1

Ta có: f(x) =(-x) =0

           f(x) =x$^{2}$ =0 

           f(0)=0

Do đó hàm số f(x) liên tục tại x=0.

2. HÀM SỐ LIÊN TỤC TRÊN MỘT KHOẢNG

Hoạt động 2:

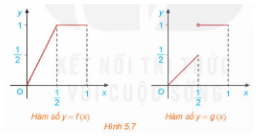
+) Hàm số f(x)={2x nếu 0≤x≤$\frac{1}{2}$1   nếu$\frac{1}{2}$<x≤1

Hàm số f(x) xác định trên [0;1], do đó x=$\frac{1}{2}$ thuộc tập xác định của hàm số.

Ta có: f(x) =1 =1

f(x) =2x =2.$\frac{1}{2}$=1

Suy ra f(x) =f(x) =1, do đó f(x) =1

Mà f($\frac{1}{2}$)=2.$\frac{1}{2}$=1 nên f(x) =f($\frac{1}{2}$)

Vậy hàm số f(x) liên tục tại x=$\frac{1}{2}$

+) Hàm số g(x)={x   nếu 0≤x≤$\frac{1}{2}$ 1   nếu$\frac{1}{2}$<x≤1

Hàm số g(x) xác định trên [0;1], do đó x=$\frac{1}{2}$ thuộc tập xác định của hàm số.

Ta có: g(x) =x =$\frac{1}{2}$

g(x) =1 =1 

=> g(x) g(x)

Vậy không tồn tại giới hạn của hàm số g(x) tại x=$\frac{1}{2}$, do đó hàm số g(x) gián đoạn tại x=$\frac{1}{2}$

+) Quan sát hình 5.7 ta thấy, đồ thị của hàm số y=f(x) là đường liền trên (0;1), còn đồ thị của hàm số y=g(x) trên (0;1) là các đoạn rời nhau.

Khái niệm

- Hàm số y=f(x) được gọi là liên tục trên khoảng (a;b) nếu nó liên tục tại mọi điểm thuộc khoảng này.

- Hàm số y=f(x) được gọi là liên tục trên đoạn [a;b] nếu nó liên tục trên khoảng (a;b) và f(x) =fa,f(x) =f(b).

- Các khái niệm hàm số liên tục trên nửa khoảng như (a;b], [a; +∞),… được định nghĩa theo cách tương tự.

Ví dụ 3: (SGK – tr.121)

Hướng dẫn giải (SGk – tr.121)

Tính liên tục của một số hàm sơ cấp đã biết

+ Hàm số đa thức và các hàm số y=sinsin x  ; y=coscos x liên tục trên R.

+ Các hàm số y=tantan x  ;y=cotcot x ;y=$\sqrt{x}$ và hàm phân thức hữu tỉ (thương của hai đa thức) liên tục trên tập xác định của chúng.

Ví dụ 4: (SGK – tr.121)

Hướng dẫn giải: (SGK – tr.121).

Luyện tập 2

Ta thấy hàm số f(x) là một hàm phân thức hữu tỉ. Vậy hàm số này liên tục trên các khoảng tập xác định của chúng: (-∞; -2) và (-2; +∞).

3. MỘT SỐ TÍNH CHẤT CƠ BẢN

Hoạt động 3:

a) Hàm số f(x)=x$^{2}$ và g(x)=-x+1 là các hàm đa thức nên nó liên tục trên R. Do đó, hai hàm số f(x) và g(x) đều liên tục tại x=1.

b) Ta có: f(x)+g(x)=x$^{2}$+(-x+1)=x$^{2}$-x+1

Do đó: L=[f(x)+g(x)]

=x$^{2}$-x+1 =1$^{2}$-1+1=1 

Lại có, f(1)=1$^{2}$=1;g(1)=-1+1=0, do đó f(1)+g(1)=1+0=1

Vậy L=f(1)+g(1)=1.

Tính chất

- Giả sử hai hàm số y=f(x) và g(x) liên tục tại điểm x$_{0}$. Khi đó:

a) Các hàm số y=f(x)+g(x), y=f(x)-g(x) và y=f(x).g(x) liên tục tại x$_{0}$;

b) Hàm số y=$\frac{f(x)}{g(x)}$ liên tục tại x$_{0}$ nếu g(x$_{0}$)≠0.

Ví dụ 5: (SGK – tr.121).

Hướng dẫn giải (SGK – tr.121).

Nhận xét

Nếu hàm số y=f(x) liên tục trên đoạn [a;b] và f(a)f(b)<0 thì tồn tại ít nhất một điểm c∈(a;b) sao cho f(c)=0

Minh họa:

Ví dụ 6: (SGK – tr.122)

Hướng dẫn giải (SGK – tr.122).

Vận dụng

Theo giả thiết, vận tốc trung bình của xe là v$_{a}$=1803=60 (km/h)

Gọi v(t) là hàm biểu thị vận tốc của xe tại thời điểm t.

Tại thời điểm xuất phát t$_{0}$, vận tốc của xe v(t$_{0}$)=0 nên có một thời điểm t$_{1}$ xe chạy với vận tốc v(t$_{1}$)>v$_{a}$

Xét hàm số f(t)=v(t)-v$_{a}$, rõ ràng ft là hàm số liên tục trên đoạn [t$_{0}$;t$_{1}$]

Ta có: f(t$_{0}$)=-v$_{a}$<0, f(t$_{1})$=v(t$_{1}$)-v$_{a}$>0 (do v(t$_{1}$)>v$_{a}$.

=> ∃ t*∈(t$_{0}$;t$_{1}$) để f(t*)=0

=> v(t*)-v$_{a}$=0⟺v(t*)=v$_{a}$=60.