CHƯƠNG I: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC

BÀI 3: CÁC CÔNG THỨC LƯỢNG GIÁC

1. CÔNG THỨC CỘNG 

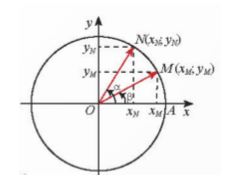
HĐKP 1

$\underset{OM}{\rightarrow}$⋅$\underset{ON}{\rightarrow}$=|$\underset{OM}{\rightarrow}$||$\underset{ON}{\rightarrow}$|cos⁡$\widehat{MON}$ (định nghĩa của tích vô hướng)

=|$\underset{OM}{\rightarrow}$||$\underset{ON}{\rightarrow}$|coscos($\alpha $-$\beta $) =coscos($\alpha $-$\beta $)

(vì $\widehat{MON}$=$\widehat{xON}$-$\widehat{xOM}$=α-β)

( vì M,N thuộc đường trò̀n lượng giác nên |$\underset{OM}{\rightarrow}$|=|$\underset{ON}{\rightarrow}$|=1). 

Vì M và N lần lượt là điểm biểu diễn của các góc lượng giác và trên đường tròn lượng giác, nên toạ độ của các điểm này là M(cos⁡β;sin⁡β) và N(cos⁡α;sin⁡α).

Do đó $\underset{OM}{\rightarrow}$⋅$\underset{ON}{\rightarrow}$=cos⁡βcos⁡α+sin⁡βsin⁡α

Vậy cos⁡(α-β)=cos⁡αcos⁡β+sin⁡αsin⁡β.

Suy ra cos⁡(α+β)=cos⁡[α-(-β)]=cos⁡αcos⁡(-β)+sin⁡αsin⁡(-β)=cos⁡αcos⁡β-sin⁡αsin⁡β.

Kết luận: Công thức cộng

cos(α+β)=coscosαcoscosβ -sinsinαsinsinβ 

cos(α-β)=coscosαcoscosβ  +sinsinαsinsinβ 

sin(α-β)=sinsinαcoscosβ   -coscosαsinsinβ 

sin(α+β)=sinsinαcoscosβ   +coscosαsinsinβ 

tantan(α-β) =$\frac{tantan\alpha -tantan\beta }{1+tantan\alpha tantan\beta }$  

tantan(α+β)=$\frac{tantan\alpha +tantan\beta }{1-tantan\alpha tantan\beta }$  

Ví dụ 1 (SGK -tr.21)

Thực hành 1

sin⁡$\frac{\pi }{12}$=sin⁡($\frac{\pi }{3}$-$\frac{\pi }{4}$)=sin⁡$\frac{\pi }{3}$cos⁡$\frac{\pi }{4}$-cos$\frac{\pi }{3}$sin⁡$\frac{\pi }{4}$=$\frac{\sqrt{3}}{2}$.$\frac{\sqrt{2}}{2}$-$\frac{1}{2}$.$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}-\sqrt{2}}{4}$;

tan$\frac{\pi }{12}$=tan⁡⁡($\frac{\pi }{3}$-$\frac{\pi }{4}$)=$\frac{tan\frac{\pi }{3}-tan\frac{\pi }{4}}{1+tan\frac{\pi }{3}tan\frac{\pi }{4}}$=$\frac{\sqrt{6}-1}{1+\sqrt{3}.1}$=2-$\sqrt{3}$

2. CÔNG THỨC NHÂN ĐÔI

HĐKP 2:

coscos2α =coscos(α+α) =coscosαcoscosα -sinsinαsinsin⁡α

=cos$^{2}$⁡α-sin$^{2}$⁡α.

Mà cos$^{2}$⁡α-sin$^{2}$⁡α=cos$^{2}$α-(1-cos$^{2}$α)=2cos$^{2}$⁡α-1.

Hoặc cos$^{2}$⁡α-sin$^{2}$⁡α=(1-sin$^{2}$⁡α)-sin$^{2}$⁡α=1-2sin$^{2}$⁡α.

+) sin⁡2α=sin⁡(α+α)=sin⁡αcos⁡α+cos⁡αsin⁡α=2sin⁡αcos⁡α.

+) tan⁡2α=tan⁡(α+α)=$\frac{tan\alpha +tan\alpha }{1-tan\alpha tan\alpha }$=$\frac{2tan\alpha }{1-tan^{2}\alpha }$

Kết luận

sinsin2α=2sinsinαcoscos⁡α   

coscos2α=α - α=2α-1=1-2α

tantan2α= $\frac{\alpha }{1-\alpha }$

Ví dụ 2 (SGK -tr.22)

Thực hành 2:

+) cos$^{2} \frac{\pi }{8}$=$\frac{cos\frac{\pi }{4}+1}{2}$=$\frac{\frac{\sqrt{2}}{2}+1}{2}$=$\frac{2+\sqrt{2}}{4}$

Vì 0<$\frac{\pi }{8}$<$\frac{\pi }{2}$ nên cos⁡$\frac{\pi }{8}$>0. Do đó cos⁡$\frac{\pi }{8}$=$\frac{\sqrt{2+\sqrt{2}}}{2}$.

+) tan$^{2} \frac{\pi }{8}$=$\frac{1}{cos^{2}\frac{\pi }{8}}$=$\frac{4}{2+\sqrt{2}}$=3-2$\sqrt{2}$.

Vì 0<$\frac{\pi }{8}$<$\frac{\pi }{2}$ nênt tan $\frac{\pi }{8}$>0. 

Do đó tan$\frac{\pi }{8}$=$\sqrt{3-2\sqrt{2}}$=$\sqrt{2}$-1.

3. CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG

HĐKP 3

a) 

cos⁡(α-β)+cos⁡(α+β)

=(cos⁡αcos⁡β+sin⁡αsin⁡β)+(cos⁡αcos⁡β-sin⁡αsin⁡β)

=2coscos⁡αcoscos⁡β   

cos⁡(α-β)-cos⁡(α+β)

=(cos⁡αcos⁡β+sin⁡αsin⁡β)-(cos⁡αcos⁡β-sin⁡αsin⁡β)

=2sin⁡αsin⁡β

b)

sinsin(α-β) +sinsin(α+β)

=(sin⁡αcos⁡β-cos⁡αsin⁡β)+(sin⁡αcos⁡β+cos⁡αsin⁡β)

=2sinsin⁡αcos cos⁡β 

sinsin(α-β) -sinsin(α+β)

=(sin⁡αcos⁡β-cos⁡αsin⁡β)-(sin⁡αcos⁡β+cos⁡αsin⁡β)

=-2cos⁡αsin⁡β.

Kết luận:

coscos⁡β  =$\frac{1}{2}$[coscos(α-β )+coscos(α+β)]

sinsinβ  =$\frac{1}{2}$[coscos(α-β] -coscos(α+β)]

sin⁡αcos⁡β=$\frac{1}{2}$[sin⁡(α-β)+sin⁡(α+β)]

Ví dụ 3 (SGK -tr.22)

Thực hành 3

sinsin $\frac{\pi }{24}$coscos $\frac{5\pi }{24}$ 

=$\frac{1}{2}$[sinsin($\frac{\pi }{24}$-$\frac{5\pi }{24}$) +sinsin( $\frac{\pi }{24}$+$\frac{5\pi }{24}$)]

=$\frac{1}{2}$[sinsin( -$\frac{\pi }{6}$) +sinsin $\frac{\pi }{4}$]

=$\frac{1}{2}$(-$\frac{1}{2}$+$\frac{\sqrt{2}}{2}$)=$\frac{-1+\sqrt{2}}{4}$

sinsin$\frac{7\pi }{8}$sinsin $\frac{5\pi }{8}$ 

=$\frac{1}{2}$[coscos( $\frac{7\pi }{8}$-$\frac{5\pi }{8}$) -coscos( $\frac{7\pi }{8}$+$\frac{5\pi }{8}$)]

=$\frac{1}{2}$[coscos $\frac{\pi }{4}$ -coscos $\frac{3\pi }{2}$]

=$\frac{1}{2}$.$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{4}$.

4. CÔNG THỨC BIẾN ĐỔI TỔNG THÀNH TÍCH

HĐKP 4

+) cos⁡$\frac{\alpha +\beta }{2}$cos⁡$\frac{\alpha -\beta }{2}$=$\frac{1}{2}$[cos⁡($\frac{\alpha +\beta }{2}$-⁡$\frac{\alpha -\beta }{2}$)+cos⁡($\frac{\alpha +\beta }{2}$+⁡$\frac{\alpha -\beta }{2}$)]=$\frac{1}{2}$(cos⁡β+cos⁡α).

+) sin$\frac{\alpha +\beta }{2}$sin⁡$\frac{\alpha -\beta }{2}$=$\frac{1}{2}$[cos($\frac{\alpha +\beta }{2}$-⁡$\frac{\alpha -\beta }{2}$)-cos(⁡$\frac{\alpha +\beta }{2}$+⁡$\frac{\alpha -\beta }{2}$)]=$\frac{1}{2}$(cos⁡β-cos⁡α).

+) sin$\frac{\alpha +\beta }{2}$cos⁡$\frac{\alpha -\beta }{2}$

=$\frac{1}{2}$[sinsin($\frac{\alpha +\beta }{2}$-⁡$\frac{\alpha -\beta }{2}$)+sinsin($\frac{\alpha +\beta }{2}$+⁡$\frac{\alpha -\beta }{2}$)]

=$\frac{1}{2}$(sin⁡β+sin⁡α)

Kết luận

cos⁡α+cos⁡β=2cos⁡$\frac{\alpha +\beta }{2}$cos⁡$\frac{\alpha -\beta }{2}$

cos⁡α-cos⁡β=-2sin⁡$\frac{\alpha +\beta }{2}$sin⁡⁡$\frac{\alpha -\beta }{2}$

sin⁡α+sin⁡β=2sin⁡$\frac{\alpha +\beta }{2}$cos⁡⁡$\frac{\alpha -\beta }{2}$

sin⁡α-sin⁡β=2cos⁡$\frac{\alpha +\beta }{2}$sin⁡⁡$\frac{\alpha -\beta }{2}$

Ví dụ 4 (SGK -tr.23)

Thực hành 4

coscos$\frac{7\pi }{12}$ +coscos$\frac{\pi }{12}$

=2cos $\frac{\frac{7\pi }{12}+\frac{\pi }{12}}{2}$cos $\frac{\frac{7\pi }{12}-\frac{\pi }{12}}{2}$ 

=2cos⁡$\frac{\pi }{3}$cos$\frac{\pi }{4}$=2⋅$\frac{1}{2}$.$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$.

Vận dụng 

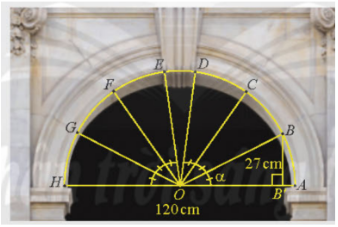
Đặt α=$\widehat{BOB'}$. Ta có sin⁡α=$\frac{BB'}{OB}$=$\frac{27}{60}$=$\frac{9}{20}$.

Vì 0<α<90$^{\circ}$ nên cos⁡α>0, suy ra cos⁡α=$\sqrt{1-sin^{2}\alpha }$=$\frac{\sqrt{319}}{20}$

Khoảng cách từ C đến AH là h$_{C}$=60⋅sin⁡2α=60.2sin⁡αcos⁡α=$\frac{27\sqrt{319}}{10}$≈48,2( cm).