CHƯƠNG I: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC

BÀI 2: GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC

1. GÍA TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC 

HĐKP 1:

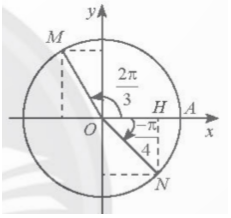
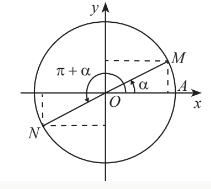
Ta có $\widehat{xOM}$=$\frac{2\pi }{3}$=120$^{\circ}$. Do đó, x$_{M}$=cos⁡120$^{\circ}$=-$\frac{1}{2}$ và y$_{M}$=sin⁡120$^{\circ}$=$\frac{\sqrt{3}}{2}$, hay M(-$\frac{1}{2}$;$\frac{\sqrt{3}}{2}$).

Ta có $\widehat{xON}$=$\frac{\pi }{4}$=45$^{\circ}$ nên △OHN là tam giác vuông cân với cạnh huyền ON=1.

Do đó OH=NH=$\frac{\sqrt{2}}{2}$. Vì N nằm trong góc phần tư thứ IV, nên ta có x$_{N}$=OH=$\frac{\sqrt{2}}{2}$ và y$_{N}$=-NH=-$\frac{\sqrt{2}}{2}$. Do đó N($\frac{\sqrt{2}}{2}$;-$\frac{\sqrt{2}}{2}$).

Kết luận 

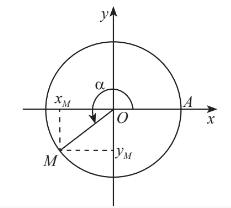
Trên đường tròn lượng giác, gọi M là điểm biểu diễn góc lượng giác có số đo . Khi đó

+ Tung độ y$_{M}$ của M gọi là sin của α, kí hiệu sin .

+ Hoành độ x$_{M}$ của M gọi là côsin của α, kí hiệu cos .

+ Nếu x$_{M}$≠0 thì tỉ số $\frac{y_{M}}{x_{M}}$=$\frac{sinsin\alpha }{coscos\alpha }$ gọi là tang của α, kí hiệu tan α .

+ Nếu yM≠0 thì tỉ số $\frac{y_{M}}{x_{M}}$=$\frac{coscos\alpha }{sinsin\alpha }$ gọi là côtang của α, kí hiệu cot α .

Các giá trị sin ,cos α ,tan ,cot    được gọi là các giá trị lượng giác của góc lượng giác α.

Chú ý:

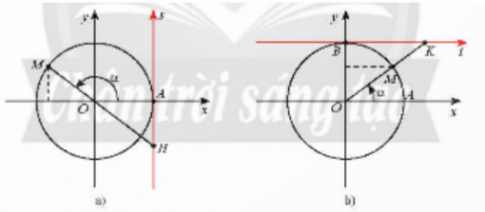
a) Ta gọi trục hoành là trục côsin, còn trục tung là trục sin.

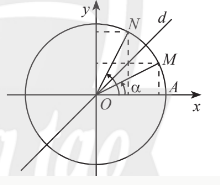
b) Trục As có gốc ở điểm A(1; 0) và song song với trục sin gọi là trục tang.

Trục Bt có gốc là điểm B(0;1) và song song với trục côsin gọi là trục côtang. 

b) sinsinα và coscosα   xác định với mọi  α∈R;

tan⁡α xác định khi α≠$\frac{\pi }{2}$+kπ(k∈Z).

cot⁡α xác định khi α≠kπ(k∈Z).

c) Với mọi góc lượng giác và số nguyên k, ta có:
sinsin (α+k2π) =sinsinα  k∈Z;

cos⁡(α+k2π)=cos⁡α (k∈Z).

tantan (α+kπ) =tantan α  (k∈Z).;

cot⁡(α+kπ)=cot⁡α (k∈Z).

d) Bảng giá trị lượng giác của một số góc lượng giác

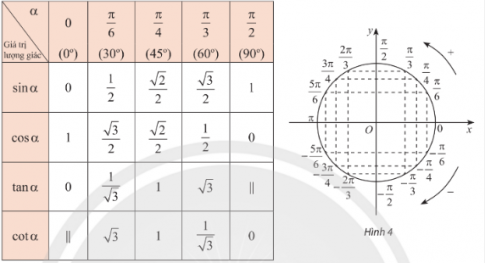
Ví dụ 1 (SGK -tr.15)

Thực hành 1

+ Vì điểm biểu diễn của hai góc -$\frac{2\pi }{3}$ và $\frac{2\pi }{3}$ trên đường tròn lượng giác đối xứng nhau qua trục hoành, nên chúng có hoành độ bằng nhau và tung độ đối nhau.

Do đó, sin(⁡-$\frac{2\pi }{3}$)=-sin(⁡$\frac{2\pi }{3}$)=-$\frac{\sqrt{3}}{2}$.
Vì 495$^{\circ}$=135$^{\circ}$+360$^{\circ}$ nên tan⁡495$^{\circ}$=tan⁡135$^{\circ}$=$\frac{sin135^{\circ}}{cos135^{\circ}}$=$\frac{-\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}$=-1

2. Tính giá trị lượng giác của một góc bằng máy tính cầm tay.

Ví dụ 2 (SGK – tr. 15)

Thực hành 2 

cos⁡75$^{\circ}$=$\frac{\sqrt{6}-\sqrt{2}}{4}$≈0,259; tan($\frac{-19\pi }{6}$)=-$\frac{\sqrt{3}}{2}$≈-0,577.

2. HỆ THỨC CƠ BẢN GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC

HĐKP 2:

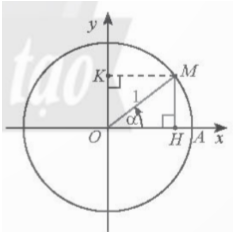
a) Trong Hình 5 , tam giác OMH vuông tại H, ta có OH=cos⁡α,MH=sin⁡α và OM=1.

Áp dụng định lí Pythagore ta có OH$^{2}$+MH$^{2}$=OM$^{2}$ hay cos$^{2}$⁡α+sin$^{2}$⁡α=1.

b) Chia cả hai vế cho cos$^{2}$⁡α(cos⁡α≠0), ta có 1+tan$^{2}$⁡α=$\frac{1}{cos^{2}\alpha }$

c) Chia cå hai vế cho sin$^{2}$⁡α(sin⁡α≠0), ta có cot$^{2}$⁡α+1=$\frac{1}{sin^{2}\alpha }$

Kết luận

$\alpha $ + $\alpha $=11+ $\alpha $=$\frac{1}{\alpha }$ (α≠$\frac{\pi }{2}$+kπ,k∈Z)1+ $\alpha $=$\frac{1}{\alpha }$ (α≠kπ,k∈Z) tan .cot =$\frac{1}{\alpha }$ (α≠k$\frac{\pi }{2}$,k∈Z)

Ví dụ 3 (SGK -tr. 17)

Thực hành 3

$\frac{1}{cos^{2}\alpha }$=1+tan$^{2}$⁡α=1+$(\frac{2}{3})^{2}$=$\frac{13}{9}$. Suy ra cos$^{2}$⁡α=$\frac{9}{13}$.

Vì π<α<$\frac{3\pi }{2}$ nên cos⁡α<0. Suy ra cos⁡α=-$\frac{3\sqrt{13}}{13}$.

Vì tan⁡α=$\frac{sin\alpha }{cos\alpha }$ nên sin⁡α=tan⁡α⋅cos⁡α=$\frac{2}{3}$-($\frac{3\sqrt{13}}{13}$)=-$\frac{2\sqrt{13}}{13}$.

3. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC LƯỢNG GIÁC CÓ LIÊN QUAN ĐẶC BIỆT

HĐKP 3:

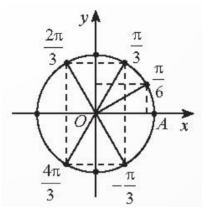
+) -α=-$\frac{\pi }{3}$

sin(⁡-$\frac{\pi }{3}$)=-sin⁡$\frac{\pi }{3}$;cos(⁡-$\frac{\pi }{3}$)=cos⁡$\frac{\pi }{3}$

tan⁡(-$\frac{\pi }{3}$)=-tan⁡$\frac{\pi }{3}$;cot⁡(-$\frac{\pi }{3}$)=-cot$\frac{\pi }{3}$.

+) α+π=$\frac{4\pi }{3}$

sin⁡$\frac{4\pi }{3}$=-sin⁡$\frac{\pi }{3}$;cos$\frac{4\pi }{3}$=-cos⁡$\frac{\pi }{3}$;

tan$\frac{4\pi }{3}$=tan⁡$\frac{\pi }{3}$;cot$\frac{4\pi }{3}$=cot⁡$\frac{4\pi }{3}$.

+) -α=$\frac{2\pi }{3}$

sinsin $\frac{2\pi }{3}$ =sinsin $\frac{\pi }{3}$ ;coscos $\frac{2\pi }{3}$ =-coscos $\frac{\pi }{3}$ ;

tan⁡$\frac{2\pi }{3}$=-tan⁡$\frac{\pi }{3}$;cot⁡$\frac{2\pi }{3}$=-cot⁡$\frac{\pi }{3}$.

+)$\frac{\pi }{2}$-α=$\frac{\pi }{6}$

sinsin$\frac{\pi }{6}$ =cossin $\frac{\pi }{3}$ ;coscos $\frac{\pi }{6}$ =sinsin $\frac{\pi }{3}$;

tan$\frac{\pi }{6}$=cot⁡$\frac{\pi }{3}$;cot⁡$\frac{\pi }{6}$=tan⁡$\frac{\pi }{3}$.

Kết luận

a) Hai góc đối nhau α và -α

coscos (-α) =coscosα  sinsin (-α) =-sinsinα tantan (-α) =-tantanα cotcot (-α) =-cotα

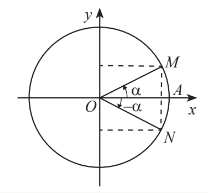
b) Hai góc hơn kém : và α+π

sinsin (π+α) =-sin⁡αcos⁡(π+α)=-cos⁡αtan⁡(π+α)=tan⁡αcot⁡(π+α)=cot⁡α

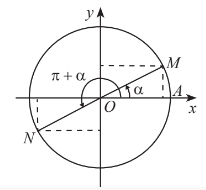
c) Hai góc bù nhau và π- α

sin⁡(π-α)=sin⁡αcos⁡(π-α)=-cos⁡αtan⁡(π-α)=-tan⁡αcot⁡(π-α)=-cot⁡α

d) Hai góc phụ nhau và $\frac{\pi }{2}$-α

sin⁡($\frac{\pi }{2}$-α)=cosαcos⁡($\frac{\pi }{2}$-α)=sin⁡αtan ($\frac{\pi }{2}$-α) =-tan⁡αcot($\frac{\pi }{2}$-α)=-cot⁡α

Ví dụ 4 (SGK -tr.18)

Thực hành 4

a) cos⁡638$^{\circ}$=cos(⁡-82$^{\circ}$+2⋅360$^{\circ}$)=cos⁡-82$^{\circ}$=cos⁡82$^{\circ}$=sin(⁡90$^{\circ}$-82$^{\circ}$)=sin⁡8$^{\circ}$;

b) cot⁡$\frac{19\pi }{5}$=cot⁡(4π-$\frac{\pi }{5}$)=cot(⁡-$\frac{\pi }{5}$)=-cot⁡$\frac{\pi }{5}$.

Vận dụng

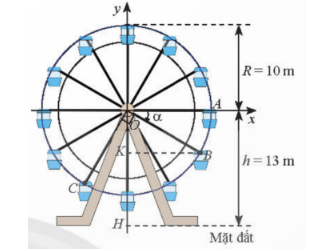
a) Tung độ của H và K lần lượt là y$_{H}$=-13 và y$_{K}$=OB⋅sin⁡(OA,OB)=10sin⁡.

Suy ra độ cao của điểm B so vói mặt đất là KH=y$_{K}$-y$_{H}$=10sin⁡$\alpha $+13.

Khi α=-30$^{\circ}$ thì KH=13+10sin⁡(-30$^{\circ}$)=8( m).

b) Ta có KH=4 hay 13+10sin⁡α=4, suy ra sin⁡α=-$\frac{9}{10}$, suy ra thuộc góc phần tư thứ III hoặc góc phần tư thứ IV. Khi đó độ cao của cabin C là h=13+10sin⁡(OA,OC)=13+10sin(⁡α-90$^{\circ}$)=13-10cos⁡α.

Trường hợp 1: thuộc góc phần tur thứ III nên cos⁡α<0.

Do đó, cos⁡α=-$\sqrt{1-sin^{2}\alpha }$=-$\frac{\sqrt{19}}{10}$.

Suy ra h=13-10⋅(-$\frac{\sqrt{19}}{10}$)≈17,36( m).

Trường hợp 2: thuộc góc phần tư thứ IV nên cos⁡α>0. Do đó, cos⁡α=$\sqrt{1-sin^{2}\alpha }$=$\frac{\sqrt{19}}{10}$.

Suy ra h=13-10⋅$\frac{\sqrt{19}}{10}$≈8,64( m).