1. GÓC HÌNH HỌC VÀ SỐ ĐO CỦA CHÚNG

HĐ1

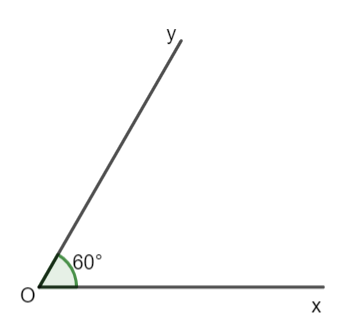
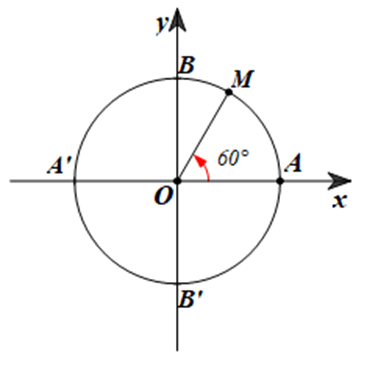
Góc (còn được gọi là góc hình học) là hình gồm hai tia chung gốc. Mỗi góc có một số đo, đơn vị đo góc (hình học) là độ. Số đo của một góc (hình học) không vượt quá 180°. Chẳng hạn: Góc xOy gồm hai tia Ox và Oy chung gốc O có số đo là 60° (hình vẽ).

• Nếu trên đường tròn, ta lấy một cung tròn có độ dài bằng bán kính thì góc ở tâm chắn cung đó gọi là góc có số đo 1 radian (hình 2).
• 1 radian còn được viết tắt là 1 rad.

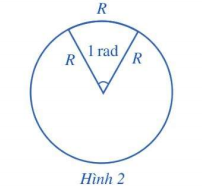
• Độ dài nửa đường tròn: πR.
• Số đo góc nửa đường tròn: 180º bằng $\frac{\pi R}{R}$ rad = π rad.
• 1 rad = $\frac{180^{o}}{\pi }$ và 1° = $\frac{\pi }{180}$ rad.

Nhận xét: Ta biết góc ở tâm có số đo 180º sẽ chắn cung bằng nửa đường tròn (có độ dài bằng πR) nên số đo góc 180º bằng $\frac{\pi R}{R}$ rad = π rad.

Do đó, 1 rad = $\frac{180^{o}}{\pi }$ ≈ 57º17'45" và 1° = $\frac{\pi }{180}$ rad ≈ 0,0175 rad 

Chú ý: Người ta thường không viết chữ radian hay rad sau số đo của góc. Chẳng hạn, $\frac{\pi }{2}$ rad cũng được viết là $\frac{\pi }{2}$.

Ví dụ 1: (SGK – tr.6).

Hướng dẫn giải (SGK – tr.6).

Luyện tập 1

2. GÓC LƯỢNG GIÁC VÀ SỐ ĐO CỦA CHÚNG

a) Khái niệm

HĐ2

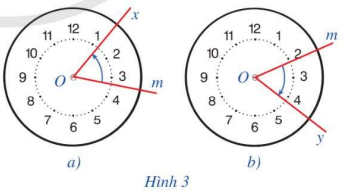
a) Chiều quay của kim đồng hồ ngược chiều với chiều quay từ tia Om đến tia Ox trong Hình 3a.

b) Chiều quay của kim đồng hồ cùng chiều với chiều quay từ tia Om đến tia Oy trong Hình 3b.

Để khảo sát việc quay tia Om quanh điểm 0 trong mặt phẳng, ta cần chọn một chiều quay gọi là chiều dương. Thông thường, ta chọn chiều dương là chiều ngược chiều quay của kim đồng hồ và chiều cùng chiều quay của kim đồng hồ gọi là chiều âm.

Kết luận: Cho hai tia Ou, Ov. Nếu tia Om quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ tia Ou đến trùng với tia Ov thì ta nói: Tia Om quét một góc lượng giác với tia đầu Ou và tia cuối Ov, kí hiệu là (Ou, Ov).

Ví dụ 2: (SGK – tr.7).

Hướng dẫn giải (SGK – tr.7).

Luyện tập 2

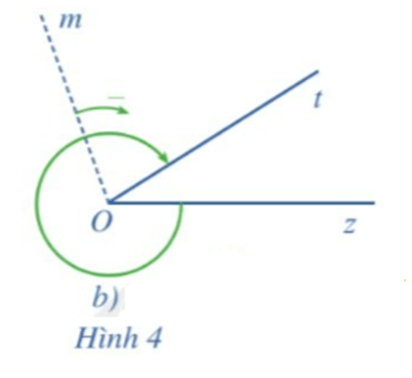
Trong Hình 4b, góc lượng giác là (Oz, Ot) với tia đầu Oz và tia cuối Ot.

HĐ3

a) 

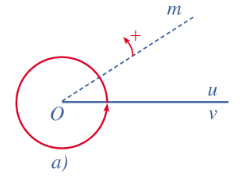
Trong Hình 5a, tia Om quay theo chiều dương đúng một vòng thì tia đó quét nên một góc 360°.

b) 

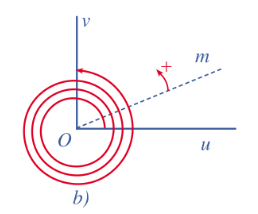
Trong Hình 5b, tia Om quay theo chiều dương ba vòng và một phần tư vòng (tức là 3$\frac{1}{4}$ vòng) thì tia đó quét nên một góc là 3$\frac{1}{4}$.360° = 1170°.

c) 

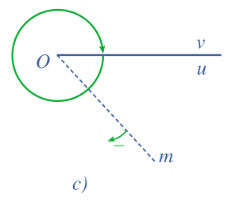
Trong Hình 5c, tia Om quay theo chiều âm đúng một vòng thì tia đó quét nên một góc là - 360°.

Nhận xét: Khi tia Om quay góc o thì góc lượng giác mà tia đó quét nên có số đo o (hay πα180rad). Vì thế, mỗi một góc lượng giác đều có một số đo, đơn vị đo góc lượng giác là độ hoặc radian. Nếu góc lượng giác (Ou, Ov) có số đo bằng thì ta kí hiệu là sđ(Ou, Ov) = hoặc (Ou, Ov) = .

Kết luận: Mỗi góc lượng giác gốc O được xác định bởi tia đầu Ou, tia cuối Ov và số đo của góc đó.

Ví dụ 3: (SGK – tr.8).

Hướng dẫn giải (SGK – tr.8).

Luyện tập 3

Ta có: $-\frac{5\pi }{4}=-\pi +\left ( -\frac{\pi }{4} \right )$

Góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo $-\frac{5\pi }{4}$ được biểu diễn ở hình vẽ dưới đây:

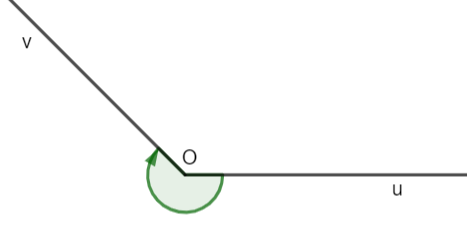
b) Tính chất

HĐ4 

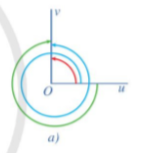
Hình 7

Hình 7b: 

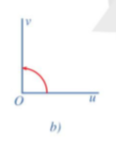
Ta thấy chiều quay của tia Ou đến Ov là chiều dương, mà Ou⊥Ov nên số đo của góc lượng giác (Ou, Ov) = 90°.

Hình 7c: 

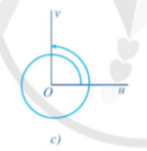
Ta thấy tia Ou quay một vòng từ Ou đến Ou, rồi quay tiếp từ Ou đến Ov theo chiều dương. Vậy số đo của góc lượng giác: 

(Ou, Ov) =360° + 90° = 450°

Hình 7d: 

Ta thấy chiều quay của tia Ou đến Ov là chiều âm và số đo góc lượng giác

(Ou, Ov) = - 270°

Nhận xét: Sự khác biệt giữa các góc lượng giác có cùng tia đầu và tia cuối chính là số vòng quay quanh điểm O. Vì vậy, sự khác biệt giữa số đo của các góc lượng giác đó chính là bội nguyên của 360° khi các góc đó tính theo đơn vị độ (hay bội nguyên của 2π rad khi các góc đó tính theo đơn vị radian).

Định lí: Nếu một góc lượng giác có số đo $\alpha ^{o}$ (hay $\alpha $ radian) thì mọi góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác đó có số đo dạng: $\alpha ^{o}+k360^{o}$ (hay α + k2π), với k là số nguyên, mỗi góc ứng với một giá trị của k.

Ví dụ 4: (SGK – tr.9).

Hướng dẫn giải SGK – tr.9.

Luyện tập 4

Gọi là số đo góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác có số đo $-\frac{4\pi }{3}$.

Ta có: $\alpha =-\frac{4\pi }{3}+k2\pi $, k ∈ Z.

HĐ5.

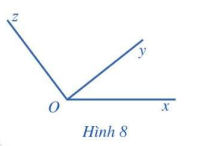
Do tia Oy nằm trong góc xOz nên: xOz = xOy + yOz

Hệ thức Chasles: Với ba tia tùy ý Ou, Ov, Ow, ta có:

(Ou, Ov) + (Ov, Ow) = (Ou, Ow) + k2π, (k ∈ Z). 

Ví dụ 5: (SGK – 9).

Hướng dẫn giải (SGK – tr.9).

Luyện tập 5

Theo hệ thức Chasles, ta có: 

(Ov, Ow) = - (Ou, Ov) + (Ou, Ow) + $k2\pi $ = $\frac{11\pi }{4}$ + $\frac{3\pi }{4}$ + $k2\pi $ = $\frac{7\pi }{2}$ + $k2\pi $ ($k\in \mathbb{Z}$).

3. ĐƯỜNG TRÒN LƯỢNG GIÁC

HĐ6

a) Đường tròn tâm O có bán kính bằng 1 (hình vẽ):

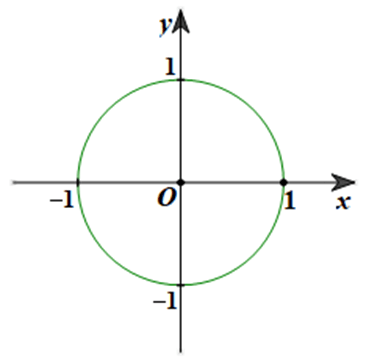
b) Chiều dương là chiều ngược với chiều quay của kim đồng hồ; chiều âm là chiều quay của kim đồng hồ.

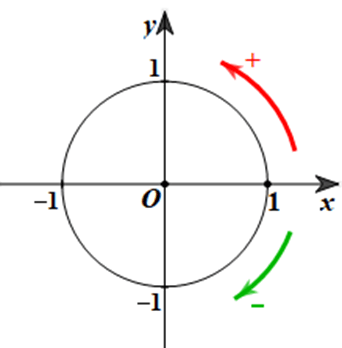
Khái niệm: Trong mặt phẳng tọa độ đã được định hướng Oxy, lấy điểm A(1; 0). Đường tròn tâm O, bán kính OA = 1 được gọi là đường tròn lượng giác (hay đường tròn đơn vị) gốc A.

Chú ý:

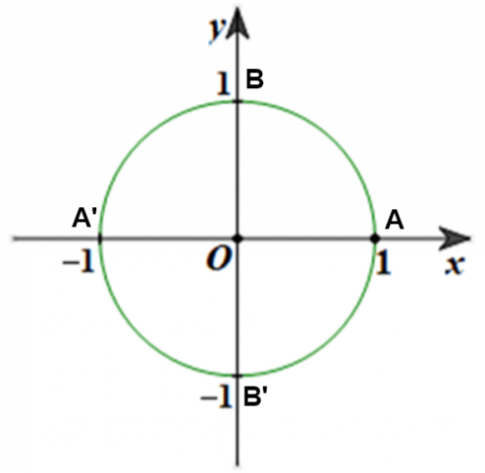
Các điểm B(0; 1), A’(-1; 0), B’(0; -1) nằm trên đường tròn lượng giác.

Ví dụ 6: (SGK – tr.10).

Hướng dẫn giải (SGK – tr.10).

Luyện tập 6

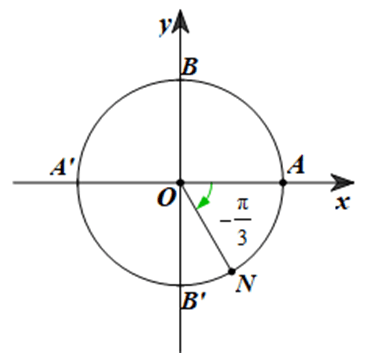
Ta có (OA, ON) = $\frac{-\pi }{3}$ là góc lượng giác có tia đầu là tia OA, tia cuối là tia ON và quay theo chiều âm (chiều quay của kim đồng hồ) một góc $\frac{\pi }{3}$.

Điểm N trên đường tròn lượng giác sao cho (OA, ON) = $-\frac{\pi }{3}$ được biểu diễn như hình dưới đây:

4. GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC

HĐ7

a) Ta có (OA, OM) = 60° là góc lượng giác có tia đầu là tia OA, tia cuối là tia OM và quay theo chiều dương một góc 60°.

Điểm M trên đường tròn lượng giác sao cho (OA, OM) = 60° được biểu diễn như hình vẽ dưới đây:

b) 

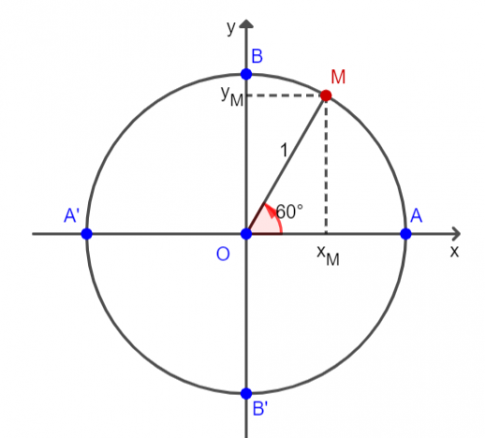
Ta có:

x_M = cos 60° .OM = cos 60° .1 

      =cos 60° = $\frac{1}{2}$

y_M = sin 60° .OM = sin 60° .1 

      = sin 60° = $\frac{\sqrt{3}}{2}$

=> Hoành độ và tung độ điểm M lần lượt bằng cos 60°  và sin 60°.

Tổng quát: Trong trường hợp tổng quát, với mỗi góc lượng giác , lấy điểm M trên đường tròn lượng giác sao cho (OA, OM) = α

Gọi tọa độ của điểm M trong hệ tọa độ Oxy là (x; y). Ta có các khái niệm sau:

• Hoành độ x của điểm M gọi là cosin của góc lượng giác α và kí hiệu cosα, cosα = x.
• Tung độ y của điểm M gọi là sin của góc lượng giác α và kí hiệu sinα, sinα = y .
• Nếu cos ≠ 0 thỉ tỉ số $\frac{sin\alpha }{cos\alpha }$ gọi là tang của góc lượng giác α và kí hiệu tanα,tanα = $\frac{sin\alpha }{cos\alpha }$
• Nếu sin ≠ 0 thì tỉ số $\frac{cos\alpha }{sin\alpha }$ gọi là cotang của góc lượng giác α và kí hiệu cotα,cotα = $\frac{cos\alpha }{sin\alpha }$.

Ví dụ 7: (SGK – tr.11).

Hướng dẫn giải (SGK – tr.11).

Luyện tập 7

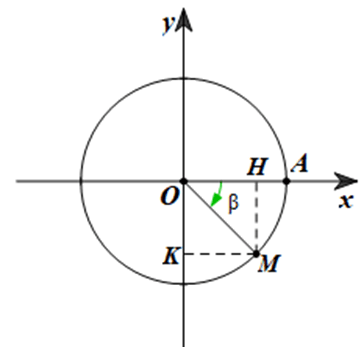
Lấy điểm M trên đường tròn lượng giác sao cho (OA, OM) = β = $-\frac{\pi }{4}=-45^{o}$

Gọi H, K lần lượt là hình chiếu của điểm M trên các trục Ox, Oy.

Khi đó, ta có: $\widehat{AOM}=45^{o}\Rightarrow \widehat{HOM}=\widehat{AOM}=45^{o}$

Theo hệ thức trong tam giác vuông HOM, ta có: 

$OH=OM.\widehat{HOM}=1.cos45^{o}=\frac{\sqrt{2}}{2}$;

$OK=MH=OM.\widehat{KOM}=1.ssin45^{o}=\frac{\sqrt{2}}{2}$

Do đó $\left ( \frac{\sqrt{2}}{2};-\frac{\sqrt{2}}{2} \right )$

Vậy $sin\left ( -\frac{\pi }{4} \right )=-\frac{\sqrt{2}}{2};cos\left ( -\frac{\pi }{4} \right )=\frac{\sqrt{2}}{2}$;

$tan\left ( -\frac{\pi }{4} \right )$ = -1; $cot\left ( -\frac{\pi }{4} \right )$ = -1.

HĐ8

Giả sử M là một điểm trên đường tròn lượng giác sao cho (OA, OM) = α = ‒30°.

Điểm M được biểu diễn như hình vẽ sau:

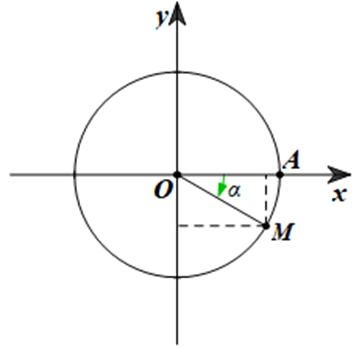
Khi đó ta có x$_{M}$ > 0 và y$_{M}$ < 0

Suy ra cosα > 0 và sinα < 0

Do đó tanα = $\frac{sin\alpha }{cos\alpha }$ < 0 và cotα = $\frac{cos\alpha }{sin\alpha }$ < 0

Dấu của các giá trị lượng giác của góc α = (OA, OM) phụ thuộc vào vị trí điểm M trên đường tròn lượng giác (Hình 12).

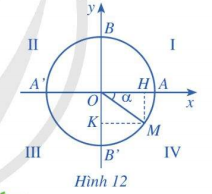
Bảng xác định dấu của các giá trị lượng giác như sau:

Ví dụ 8: (SGK – tr.11).

Hướng dẫn giải (SGK – tr.11).

Luyện tập 8

Giả sử điểm M trên đường tròn lượng giác sao cho α = $\frac{5\pi }{6}$.

Do $\frac{\pi }{2}<\frac{5\pi }{6}<\pi $ nên điểm M nằm trong góc phần tư thứ II.

Do đó sin$\frac{5\pi }{6}$ > 0;cos$\frac{5\pi }{6}$ < 0; tan$\frac{5\pi }{6}$ < 0; cot$\frac{5\pi }{6}$ < 0. 

HĐ9

a) 

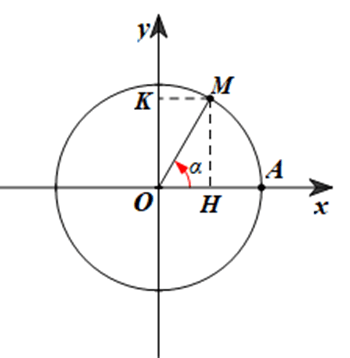
Lấy điểm M trên đường tròn lượng giác sao cho (OA, OM) = α (hình vẽ).

Gọi H, K lần lượt là hình chiếu của điểm M trên các trục Ox, Oy.

Khi đó ta có $\widehat{AOM}$ = α.

Xét ∆OMH vuông tại H, theo định lí Pythagore ta có:

OM$^{2}$ = OH$^{2}$ + MH$^{2}$ 

=> $1^{2}=cos^{2}\alpha +sin^{2}\alpha $.

b) Ta có: $tan\alpha =\frac{sin\alpha }{cos\alpha }$; $v$, (với cosα ≠ 0,sinα ≠ 0).

=> $tan\alpha .cot\alpha =\frac{sin\alpha }{cos\alpha }.\frac{cos\alpha }{sin\alpha }$ = 1.

c) Với cosα ≠ 0, ta có:

$1+tan^{2}\alpha =1+\left (\frac{sin\alpha }{cos\alpha }  \right )^{2}=\frac{cos^{2}\alpha +sin^{2}\alpha }{cos^{2}\alpha }=\frac{1}{cos^{2}\alpha }$ (do $sin^{2}\alpha +cos^{2}\alpha $ = 1).

d) Với sin ≠0, ta có:

$1+cot^{2}\alpha =1+\left (\frac{cos\alpha }{sin\alpha }  \right )^{2}=\frac{sin^{2}\alpha +cos^{2}\alpha }{sin^{2}\alpha }=\frac{1}{sin^{2}\alpha }$ (do $cos^{2}\alpha +sin^{2}\alpha $ = 1).

Công thức

• $cos^{2}\alpha +sin^{2}\alpha $ = 1 với mọi α.
• $tan\alpha =\frac{1}{cot\alpha }$ với cosα, sinα ≠ 0.
• $1+tan^{2}\alpha =\frac{1}{cos^{2}\alpha }$ với cosα ≠ 0.
• $1+cot^{2}\alpha =\frac{1}{sin^{2}\alpha }$ với sinα ≠ 0.

Ví dụ 9: (SGK – tr.12).

Hướng dẫn giải (SGK – tr.12).

Luyện tập 9

Do $\pi < \alpha < \frac{3\pi }{2}$ nên $cos\alpha < 0 $.

Áp dụng công thức $cos^{2}\alpha + sin^{2}\alpha = 1$ với mọi $\alpha $, ta có:

$cos^{2}\alpha = 1 - sin^{2}\alpha =  1 - \left ( -\frac{4}{5} \right )^{2}= \frac{9}{25}$

Suy ra $cos\alpha = -\frac{3}{5}$.

HĐ10

Bảng lượng giác của một số góc

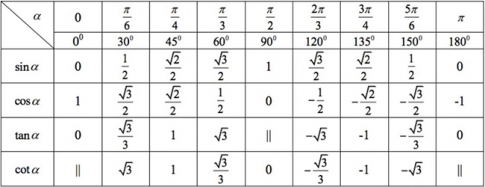
Ví dụ 10: (SGK – tr.12).

Hướng dẫn giải (SGK – tr.12).

Luyện tập 10

Ta có: $Q = tan^{2}\frac{\pi }{3} + sin^{2}\frac{\pi }{4}+cot\frac{\pi }{4}+cos\frac{\pi }{2} = \left ( \sqrt{3} \right )^{2} + \left ( \frac{\sqrt{2}}{2} \right )^{2} + 1 + 0 = \frac{9}{2} $.

5. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC CÓ LIÊN QUAN ĐẶC BIỆT

HĐ11

a) Nhận xét: $x_{M}=x_{M'}$ và $y_{M}=-y_{M'}$.

b) Do $x_{M}=x_{M'}$ nên cosα = cos(-α ).

Do $y_{M}=-y_{M'}$ nên sinα = -sin(-α)

Khi đó: 

• $tan\alpha =\frac{sin\alpha }{cos\alpha }=-\frac{sin(-\alpha )}{cos(-\alpha )}=-tan(-\alpha )$
• $cot\alpha =\frac{1}{tan\alpha }=\frac{1}{-tan(-\alpha )}=-cot(-\alpha )$

Công thức:

• Hai góc đối nhau (α và -α)

$sin(-\alpha )=-sin(-\alpha );cos(-\alpha )=cos\alpha $

$tan\alpha =-tan(-\alpha );cot\alpha =-cot(-\alpha )$

• Hai góc hơn kém nhau (α và α + π)

sin(α+π) = -sinα; tan(α+π) = tanα

cos(α+π) = -cosα; cot(α+π) = cotα

• Hai góc bù nhau (α và π - α)

sin(π - α) = sinα; cos(π - α) = -cosα; 

tan(π - α) = -tanα; cot(π - α) = -cotα. 

• Hai góc phụ nhau (α và $\frac{\pi }{\alpha }$)

sin($\frac{\pi }{\alpha }$) = cosα; tan($\frac{\pi }{\alpha }$) = cotα;

cos($\frac{\pi }{\alpha }$) = sinα; cot($\frac{\pi }{\alpha }$) = tanα.

Ví dụ 11: (SGK – tr.14).

Hướng dẫn giải (SGK – tr.14).

Luyện tập 11

a) $cos^{2}\frac{\pi }{8} + cos^{2}\frac{3\pi }{8} = cos^{2}\left (\frac{\pi }{2} - \frac{3\pi }{8}\right ) + cos^{2}\frac{3\pi }{8} = sin^{2}\frac{3\pi }{8} + cos^{2}\frac{3\pi }{8} = 1$

b) $ tan1^{\circ} . tan2^{\circ} . tan45^{\circ} . tan88^{\circ} . tan89^{\circ}$

    $= cot\left ( 90^{\circ} - 1^{\circ} \right  ).cot\left ( 90^{\circ} - 2^{\circ} \right  ). tan45^{\circ}.tan88^{\circ} . tan89^{\circ}$

    $= cot89^{\circ} . cot88^{\circ}.tan45^{\circ} . tan88^{\circ} . tan89^{\circ}$

    $= cot89^{\circ} . tan89^{\circ}.cot88^{\circ}.tan88^{\circ}.tan45^{\circ}$

    $= tan45^{\circ} = 1 $. 

6. SỬ DỤNG MÁY TÍNH CẦM TAY ĐỂ TÍNH GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC

Nếu đơn vị của góc lượng giác là độ (º), trước hết, ta chuyển máy tính sang chế độ “độ”.

Nếu đơn vị của góc lượng giác là radian (rad), trước hết, ta chuyển máy tính sang chế độ “radian”.

Ví dụ 12: (SGK – tr.14).

Hướng dẫn giải (SGK – tr.15).

Luyện tập 12

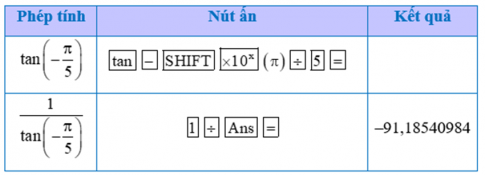
a) $tan\left ( -75^{\circ} \right )$

b) ta có: $cot\left (-\frac{\pi }{5}\right )=\frac{1}{tan\left (-\frac{\pi }{5}\right )}$