B. Hoạt động hình thành kiến thức

1. Thực hiện các hoạt động sau để hiểu về khoảng cách giữa hai đường thẳng song song 

a) Đọc và thực hiện

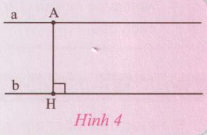
Cho hai đường thẳng a và b song song với nhau. Gọi A và B là hai điểm bất kì thuộc đường thẳng a. AH và BK là các đường vuông góc kẻ từ A và B đến đường thẳng b (Hình 3).

Đo độ dài AH và BK. Nêu nhận xét.

Trả lời:

Sau khi đo AH và BK, ta thấy hai đoạn thẳng này có độ dài bằng nhau.

b) Đọc kĩ nội dung sau

• Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia

c) Cho tứ giác ABKH có bốn góc vuông, AH = b và AB = a (Hình 5).

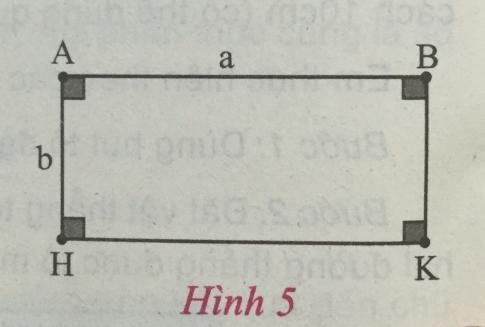
Khi đó AB // HK và AH // BK.

Suy ra khoảng cách giữa hai đường thẳng AB và HK chính là khoảng cách từ điểm A đến đường thẳng HK bằng AH và bằng b.

Tương tự hãy tính khoảng cách giữa hai đường thẳng AH và BK.

Trả lời:

Vì AH // BK nên suy ra khoảng cách giữa hai đường thẳng AH và BK chính là khoảng cách từ điểm A đến đường thẳng BK bằng AB và bằng a.

2. Thực hiện các hoạt động sau để hiểu về tính chất khoảng cách giữa hai đường thẳng song song

a) Đọc và thực hiện

Cho đường thẳng b. Gọi a và a' là hai đường thẳng song song với đường thẳng b và cùng cách đường thẳng b một khoảng bằng 5cm (Hình 6). Gọi (I) và (II) là các nửa mặt phẳng đối nhau có bờ b. Gọi M và M' là các điểm cách đường thẳng b một khoảng bằng 5cm, trong đó M thuộc nửa mặt phẳng (I), M' thuộc nửa mặt phẳng (II). Kiểm tra xem điểm M có thuộc đường thẳng a không, điểm M' có thuộc đường thẳng a' không?

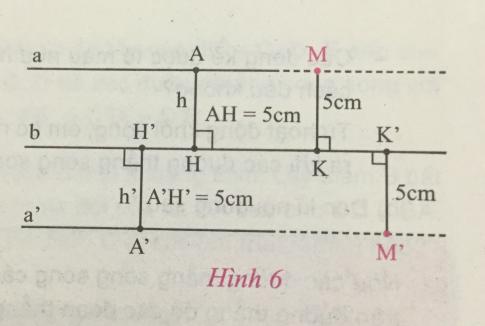
Trả lời: 

Sau khi kiểm tra, ta thấy M có thuộc đường thẳng a, điểm M' có thuộc đường thẳng a'.

b) Đọc kĩ nội dung sau

• Các điểm cách đường thẳng b một khoảng h nằm trên hai đường thẳng song song với b và cách b một khoảng h.

3. Thực hiện các hoạt động sau để hiểu về các đường thẳng song song cách đều

a) Đọc nội dung sau và trả lời câu hỏi

• Các dòng kẻ được tô màu như hình 1 có phải là các đường thẳng song song cách đều không?

• Từ hoạt động khởi động, em có nhận xét gì về độ dài các đoạn thẳng được tạo ra khi các đường thẳng song song cách đều cắt một đường thẳng?

Trả lời:

• Các dòng kẻ được tô màu như hình 1 có là các đường thẳng song song cách đều.
• Từ hoạt động khởi động, em có thể nhận xét đưa ra nhận xét sau: "Các đoạn thẳng được tạo ra khi các đường thẳng song song cách đều cắt một đường thẳng có độ dài bằng nhau".

b) Đọc kĩ nội dung sau

c) Tính độ dài đoạn thẳng AE biết đoạn BC dài 7cm (Hình 9).

Trả lời:

Ta có: AH, BI, CJ, DK, EL cùng vuông góc với HL và khoảng cách giữa AH và BI, BI và CJ, CJ và DK, DK và EL lại bằng nhau nên AH, BI, CJ, DK, EL là các đoạn thẳng song song cách đều nhau.

Từ đó suy ra AB = BC = CD = DE.

Như vậy, ta có: AE = AB + BC + CD + DE = 4.BC = 4.7 = 28 (cm).