A. B. Hoạt động khởi động và hình thành kiến thức

1. a) Thực hiện các yêu cầu sau

• Thực hiện phép nhân đa thức: 

1. (3x$^{2}$ - 2x – 3).(x$^{2}$ - 4x + 2);
2. (9x$^{2}$ + 6x + 4).(3x – 2).

Trả lời:

(3x$^{2}$ - 2x – 3).(x$^{2}$ - 4x + 2) = 3x$^{4}$ - 12x$^{3}$ + 6x$^{2}$ - 2x$^{3}$ + 8x$^{2}$ - 4x – 3x$^{2}$ + 12x – 6

                                           = 3x$^{4}$ - 14x$^{3}$ + 11x$^{2}$ + 8x - 6;

(9x$^{2}$ + 6x + 4).(3x – 2) = 27x$^{3}$ + 18x$^{2}$ + 12x – 18x$^{2}$ - 12x – 8 = 27x$^{3}$ - 8.

• Thực hiện phép chia 962 cho 26 theo cột dọc.

Trả lời:

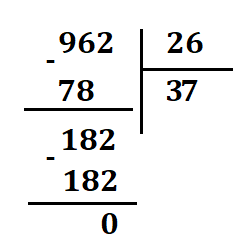
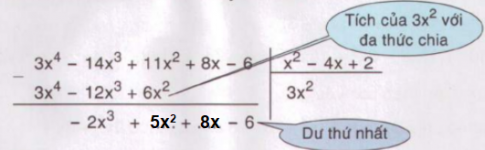
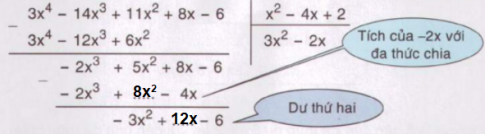
• Xét phép chia đa thức 3x$^{4}$ - 14x$^{3}$ + 11x$^{2}$ + 8x – 6 cho đa thức. Tương tự phép chia số tự nhiên, hãy điền vào chỗ trống (...) để hoàn thành phép chia:

Trả lời:

b) Làm phép chia:

(x3 – x2 - 7x + 2) : (x – 3);

(36x + 12x5 - 8x4 + 10x3 - 6x2 + 2x – 1) : (x4 + 4x3 - 3x2 + 2x – 1)

Trả lời

Có: 36x + 12x5 - 8x4 + 10x3 - 6x2 + 2x – 1 = 12x5 - 8x4 + 10x3 - 6x2 + 38x – 1

Nên (36x + 12x5 - 8x4 + 10x3 - 6x2 + 2x – 1) : (x4 + 4x3 - 3x2 + 2x – 1)

= (12x5 - 8x4 + 10x3 - 6x2 + 38x – 1) : (x4 + 4x3 - 3x2 + 2x – 1).

Ta có:

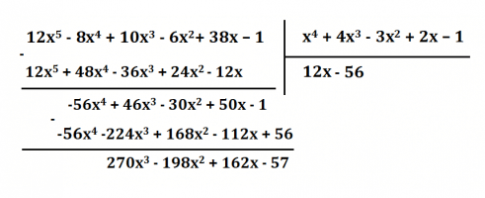
c) Làm phép chia:

• (x$^{3}$ - x$^{2}$ - 7x + 2) : (x – 3);
• (36x + 12x$^{5}$ - 8x$^{4}$ + 10x$^{3}$ - 6x$^{2}$ + 2x – 1) : (x$^{4}$ + 4x$^{3}$ - 3x$^{2}$ + 2x – 1).

Trả lời:

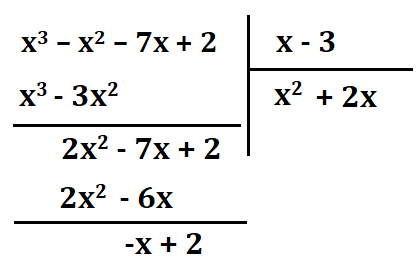
• Có: 36x + 12x$^{5}$ - 8x$^{4}$ + 10x$^{3}$ - 6x$^{2}$ + 2x – 1 = 12x$^{5}$ - 8x$^{4}$ + 10x$^{3}$ - 6x$^{2}$ + 38x – 1

Nên (36x + 12x$^{5}$ - 8x$^{4}$ + 10x$^{3}$ - 6x$^{2}$ + 2x – 1) : (x$^{4}$ + 4x$^{3}$ - 3x$^{2}$ + 2x – 1)

     = (12x$^{5}$ - 8x$^{4}$ + 10x$^{3}$ - 6x$^{2}$ + 38x – 1) : (x$^{4}$ + 4x$^{3}$ - 3x$^{2}$ + 2x – 1).

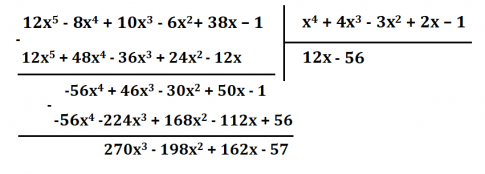
2. a) Thực hiện các theo yêu cầu 

• Xét phép chia 27x$^{3}$ + 5x - 6 cho đa thức 9x$^{2}$ + 6x + 4. Điền vào chỗ trống (....) để thực hiện phép chia.

Trả lời:

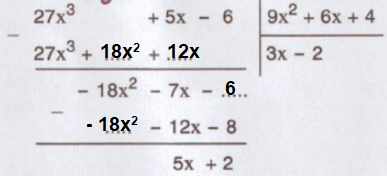
b) Đọc kĩ nội dung sau

Phép chia hai đa thức đã sắp xếp được thực hiện tương tự như phép chia hai sô tự nhiên:

• Chia hạng tử bậc cao nhất của đa thức bị chia cho hạng tử bậc cao nhất của đa thức chia, được hạng tử bậc cao nhất của thương.
• Chia hạng tử bậc cao nhất của dư thứ nhất cho hạng tử bậc cao nhất của đa thức chia, được hạng tử thứ hai của thương.
• Quá trình trên được tiếp tục khi được dư cuối cùng bằng 0 (phép chia hết) hoặc dư cuối cùng khác 0 có bậc thấp hơn bậc của đa thức chia (phép chia có dư).

c) Cho hai đa thức A = 3x$^{4}$ + x$^{3}$ - 6x – 4 và B = x$^{2}$ + 1. Tìm dư R trong phép chia A cho B rồi viết A dưới dạng A = B.Q + R.

Trả lời:

Như vậy, ta có R = -7x – 1 và Q = 3x$^{2}$ + x – 3 nên A = (x$^{2}$ + 1).(3x$^{2}$ + x – 3) + (-7x – 1).