Giải VNEN toán 8 bài 3: Những hằng đẳng thức đáng nhớ
Giải bài 3: Những hằng đẳng thức đáng nhớ - Sách VNEN toán 8 tập 1 trang 10. Phần dưới sẽ hướng dẫn trả lời và giải đáp các câu hỏi trong bài học. Cách làm chi tiết, dễ hiểu. Hi vọng các em học sinh nắm tốt kiến thức bài học.
A. B. Hoạt động khởi động và hình thành kiến thức
1. a) Thực hiện các yêu cầu:
- Với a và b là hai số bất kì, tính (a + b)(a + b).
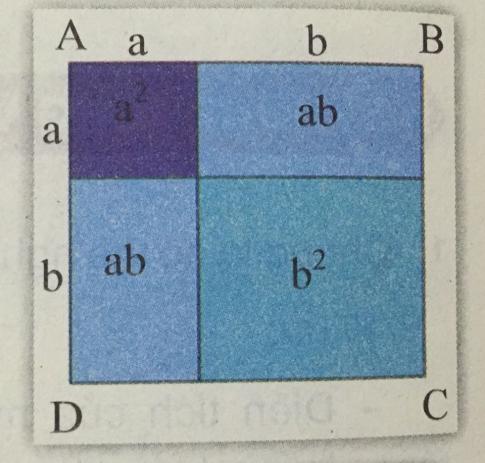
- Với a > 0; b > 0, hãy tính tích (a + b)(a + b) thông qua việc tính diện tích hình vuông ABCD theo hai cách.
Trả lời:
- Với a ,b là hai số bất kì, ta có:
(a + b)(a + b) = a$^{2}$ + ab + ba + b$^{2}$ = a$^{2}$ + 2ab + b$^{2}$.
- Với a > 0; b > 0, ta có thể tính diện tích ABCD theo hai cách như sau:
Cách 1: S$_{ABCD}$ = (a + b)(a + b)
Cách 2: S$_{ABCD}$ = a$^{2}$ + ab + ba + b$^{2}$ = a$^{2}$ + 2ab + b$^{2}$
Như vậy, qua việc tính diện tích hình vuông ABCD theo hai cách như trên, ta có thể suy ra tích
(a + b)(a + b) = a$^{2}$ + ab + ba + b$^{2}$ = a$^{2}$ + 2ab + b$^{2}$.
b) Đọc kĩ nội dung sau
Bình phương của một tổng:
- Với A, B là các biểu thức tùy ý, ta có: (A + B)$^{2}$ = A$^{2}$ + 2AB + B$^{2}$
c) Thực hiện các yêu cầu:
- Tính (2b + 1)$^{2}$.
- Điền chữ, số thích hợp vào chỗ chấm để viết biểu thức x$^{2}$ + 4x + 4 dưới dạng bình phương của một tổng: x$^{2}$ + 4x + 4 = x$^{2}$ + 2.x.2 + 2$^{2}$ = ……………………………..
- Tính nhanh 401$^{2}$.
Trả lời:
- Có: (2b + 1)$^{2}$ = (2b)$^{2}$ + 2.2b.1 + 1$^{2}$ = 4b$^{2}$ + 4b + 1.
- Có: x$^{2}$ + 4x + 4 = x$^{2}$ + 2.x.2 + 2$^{2}$ = …(x + 2)$^{2}$ …
- 401$^{2}$ = (400 + 1)$^{2}$ = 400$^{2}$ + 2.400.1 + 1$^{2}$ = 160000 + 800 + 1 = 160801.
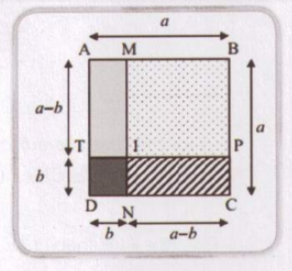
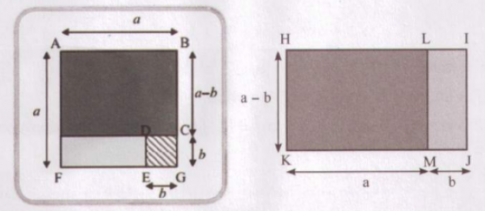
2. a) Với a, b là hai số bất kì, hãy điền vào chỗ chấm để tính (a – b)$^{2}$ theo hai cách:
Cách 1: (a – b)$^{2}$ = [a + (-b)]$^{2}$ = a$^{2}$ + 2.a.(-b) + (-b)$^{2}$ = ……………………;
Cách 2: (a – b)(a – b) = ……………………… = ………………………………
Trả lời:
Cách 1: (a – b)$^{2}$ = [a + (-b)]$^{2}$ = a$^{2}$ + 2.a.(-b) + (-b)$^{2}$ = a$^{2}$ - 2ab + b$^{2}$;
Cách 2: (a – b)(a – b) = a$^{2}$ - ab - ba + b$^{2}$ = a$^{2}$ - 2ab + b$^{2}$.
b) Đọc kĩ nội dung sau
Bình phương của một hiệu:
- Với A, B là các biểu thức tùy ý, ta có: (A - B)$^{2}$ = A$^{2}$ - 2AB + B$^{2}$
c) Thực hiện các yêu cầu:
- Tính (2x – y)$^{2}$.
- Tính nhanh 999$^{2}$.
Trả lời:
- Có: (2x – y)$^{2}$ = (2x)$^{2}$ - 2.2x.y + y$^{2}$ = 4x$^{2}$ - 4xy + y$^{2}$.
- Có: 999$^{2}$ = (1000 – 1)$^{2}$ = 1000$^{2}$ - 2.1000.1 + 1$^{2}$ = 1000000 – 2000 + 1 = 998001.
3. a) Với a, b bất kì, tính (a + b)(a – b).
Trả lời:
(a + b)(a – b) = a$^{2}$ - ab + ba - b$^{2}$ = a$^{2}$ - b$^{2}$.
b) Đọc kĩ nội dung sau
Hiệu hai bình phương:
- Với A, B là các biểu thức tùy ý, ta có: A$^{2}$ - B$^{2}$ = (A + B)(A - B)
c) Thực hiện các yêu cầu:
- Tính (x – 2y)(x + 2y).
- Tính nhanh 77.83.
Trả lời:
- Có: (x – 2y)(x + 2y) = x$^{2}$ - (2y)$^{2}$ = x$^{2}$ - 4y$^{2}$.
- Có: 77.83 = (80 – 3)(80 + 3) = 80$^{2}$ - 3$^{2}$ = 6400 – 9 = 6391.

Bình luận