A. Hoạt động khởi động

Thực hiện đo đạc

Bác Ba muốn tính khoảng cách giữa hai vị trí ở hai bên bờ ao cá. Để làm điều đó bác đã thực hiện đo đạc và vẽ mô phỏng theo tỉ lệ 1 : 600 như hình 16.

Em hãy giúp bác Ba tính khoảng cách giữa hai vị trí A và B ở hai bên bờ ao cá nhé!

Trả lời:

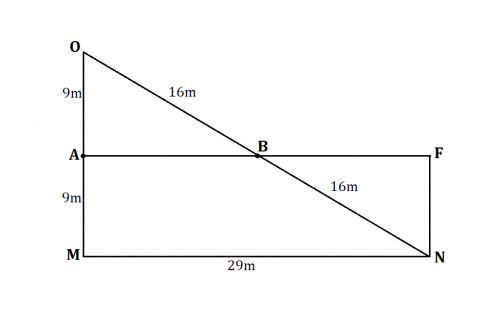
Vẽ điểm F sao cho B là trung điểm của AF.

Dễ dàng nhận thấy: $\Delta$AOB = $\Delta$FNB (c.g.c) $\Rightarrow$ AO = FN và $\widehat{O}$ = $\widehat{N}$.

Ta có: OA = AM (gt) và OA = FN $\Rightarrow$ AM = FN.

Lại có $\widehat{O}$ = $\widehat{N}$ mà hai góc này ở vị trí so le trong nên AO // FN.

$\Rightarrow$ AM // FN $\Rightarrow$ AMNF là hình thang.

Hình thang AMNF có hai đáy AM và FN bằng nhau nên hai cạnh bên AF và MN song song và bằng nhau.

$\Rightarrow$ AB // MN, AB = $\frac{1}{2}$AF = $\frac{1}{2}$MN.

Như vậy, độ dài đoạn AB sẽ bằng 14,5m.

B. Hoạt động hình thành kiến thức

1. Thực hiện theo yêu cầu

a) Thực hiện theo các bước sau

- Vẽ tam giác ABC.

- Lấy M là trung điểm của AB.

- Từ M kẻ đường thẳng song song với cạnh BC cắt cạnh AC ở N.

Em dùng thước đo độ dài các đoạn AN, CN và dự đoán vị trí điểm N trên cạnh AC.

Trả lời:

Độ dài của các đoạn AN, CN được thể hiện ở hình vẽ dưới đây.

Vị trí điểm N có thể trùng với trung điểm của đoạn thẳng AC.

b) Đọc kĩ nội dung sau

• Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba.

c) Luyện tập

Em thực hiện chứng minh kết quả trên với giả thiết cạnh thứ hai là AB, N là trung điểm cạnh AC, NP song song với AB. Ta chứng minh P là trung điểm của BC. Em hãy điền vào chỗ chấm (…) để hoàn thiện chứng minh trong lời giải sau:

Từ A kẻ đường thẳng song song với BC cắt đường thẳng PN tại M.

Xét $\Delta$ABP và $\Delta$PMA ta có:

• … (chung)
• $\widehat{BAP}$ = $\widehat{MPA}$ (do …)
• $\widehat{APB}$ = … (do …)

$\Rightarrow$ $\Delta$ABP = $\Delta$PMA (…)$\Rightarrow$ BP = MA (1)

Xét $\Delta$AMN và $\Delta$CPN ta có:

• AN = … (do …)
• $\widehat{NAM}$ = $\widehat{NCP}$ (do …)
• …  = … (do 2 góc đối đỉnh)

$\Rightarrow$ $\Delta$AMN = $\Delta$CPN (…)$\Rightarrow$ AM = CP (2)

Từ (1) và (2) suy ra BP = CP hay P là … của BC.

Trả lời:

Từ A kẻ đường thẳng song song với BC cắt đường thẳng PN tại M.

Xét $\Delta$ABP và $\Delta$PMA ta có:

• AP (chung)
• $\widehat{BAP}$ = $\widehat{MPA}$ (do so le trong)
• $\widehat{APB}$ = $\widehat{APB}$ (do so le trong)

$\Rightarrow$ $\Delta$ABP = $\Delta$PMA (g.c.g) $\Rightarrow$ BP = MA (1)

Xét $\Delta$AMN và $\Delta$CPN ta có:

• AN = NC (do N là trung điểm AC (gt))
• $\widehat{NAM}$ = $\widehat{NCP}$ (do so le trong)
• $\widehat{ANM}$ = $\widehat{CNP}$ (do 2 góc đối đỉnh)

$\Rightarrow$ $\Delta$AMN = $\Delta$CPN (g.c.g) $\Rightarrow$ AM = CP (2)

Từ (1) và (2) suy ra BP = CP hay P là trung điểm của BC.

2. Thực hiện theo yêu cầu

a) Quan sát hình 19, rút ra nhận xét về vị trí tương đối và tương quan độ dài của MN và BC:

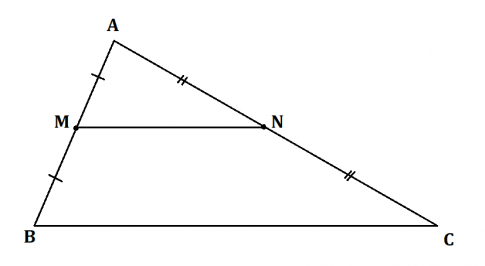
Trả lời:

Quan sát hình 19, ta có thể đưa ra nhận xét: MN // BC và MN = $\frac{1}{2}$BC.

b) Đọc kĩ nội dung sau

• Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
• Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

c) Sử dụng định lí về đường trung bình của tam giác để tính khoảng cách giữa hai vị trí bờ ao cá và kiểm nghiệm lại kết quả đo đạc ban đầu của em (hình 16).

Trả lời:

Theo định lí đường trung bình, ta có: AB = $\frac{1}{2}$MN = $\frac{1}{2}$.29 = 14,5 (m).

Như vậy, kết quả tính toán ở phần khởi động là chính xác.