BÀI 2. TẬP HỢP

1. NHẮC LẠI VỀ TẬP HỢP

Bài 1: 

a. Lấy ba ví dụ về tập hợp và chỉ ra một số phần tử của chúng.

b. Với mỗi tập hợp N, Z, Q, R, hãy sử dụng lí hiệu ∈, ∉ để chỉ ra các phần tử thuộc, hai phần tử không thuộc tập hợp đó.

Đáp án chuẩn:

a. A = {1; 2; 3; 4; 5} => Các phần tử: 1; 2; 3; 4; 5

B = {-30; -20; -10; 0; 10; 20; 30}=> Các phần tử: -30; -20; -10; 0; 10; 20; 30

C = {Vật lí, Hóa học, Toán học}=> Các phần tử: Vật lí, Hóa học, Toán học.

Bài 2: Viết các tập hợp sau đây dưới dạng liệt kê các phần tử và tìm số phần tử của mỗi tập hợp đó:

Đáp án chuẩn:

a. A = {1; 2; 3; 4; 6; 8; 12; 24} có 8 phần tử

b. B = {0; 1; 3; 5} có 4 phần tử

c. C = {0; 5; 10; 15; 20; 25; 30} có 7 phần tử

d. D = Ø không có phần tử nào

Bài 3: Viết các tập hợp sau đây dưới dạng chỉ ra tính chất đặc trưng cho các phần tử:

a. A = {1; 3; 5; ... ; 15}

b. B = {0; 5; 10; 15; 20; ...}

c. Tập hợp C các nghiệm của bất phương trình 2x + 5 > 0

Đáp án chuẩn:

a. A = {x ∈N| x là Ư (15)}

b. B = {x ∈N| x là B (5)}

c. C = {x ∈R| 2x + 5 > 0}

2. TẬP CON VÀ HAI TẬP HỢP BẰNG NHAU

Bài 1: Trong mỗi trường hợp sau đây, các phần tử của tập hợp A có thuộc tập hợp B không? Hãy giải thích.

a. A = {-1; 1} và B = {-1; 0; 1; 2}

b. A = N và B = Z 

c. A là tập hợp các học sinh nữ của lớp 10E, B là tập hợp các học sinh của lớp này.

d. A là tập hợp các loài động vật có vú, B là tập hợp các loài động vật có xương sống.

Đáp án chuẩn:

a. A ∈ B 

b. A ∈ B 

c. A ∈ B 

d. A ∈ B

Bài 2: Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập hợp con của tập hợp còn lại? Chúng có bằng nhau không?

Đáp án chuẩn:

a. A = B

b. D ⊂ C

c. E ⊂ F

Bài 3: Viết tất cả các tập hợp con của tập hợp A = {a; b}

Đáp án chuẩn:

M = {a}; N = {b}

Bài 4: Bạn An khẳng định rằng: Với các tập hợp A, B, C bất kì, nếu A ⊂ B và B ⊂ C thì A ⊂ C. Khẳng định của bạn An có đúng không? Hãy giải thích băng cách sử dụng biểu đồ Ven.

Đáp án chuẩn:

Đúng

3. MỘT SỐ TẬP CON CỦA TẬP HỢP SỐ THỰC

Bài 1: Dùng các kí hiệu đoạn, khoảng, nửa khoảng để viết các tập hợp sau đây:

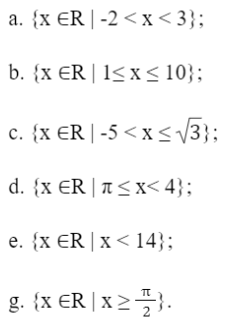
Đáp án chuẩn:

BÀI TẬP CUỐI SGK

Bài 1:  Viết các tập hợp sau đây dưới dạng liệt kê các phần tử:

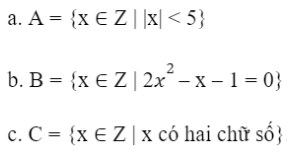
Đáp án chuẩn:

a. A = {-4; -3; -2; -1; 0; 1; 2; 3; 4}

b. B = {−12; 1}

c. C = {10; 11; 12; 13;...; 98; 99}

Bài 2: Viết các tập hợp sau đây dưới dạng chỉ ra tính chất đặc trưng cho các phần tử:

a. Tập hợp A = {1; 2; 3; 6; 9; 18};

b. Tập hợp B các nghiệm của bất phương trình 2x  + 1 > 0;

c. Tập hợp C các nghiệm của phương trình 2x - y = 6.

Đáp án chuẩn:

a. A = {x ∈N | x là Ư(18)}

b. B = {x ∈R | 2x + 1 > 0}

c. C = {x ∈R, y ∈R | 2x - y = 6}

Bài 3: Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập hợp con của tập còn lại? Chúng có bằng nhau không?

Đáp án chuẩn:

a. A = B

b. C ⊂ D

c. E ⊂ F

Bài 4. Hãy viết tất cả tập hợp con của tập hợp B = {0; 1; 2}

Đáp án chuẩn:

C = {0}; D = {1}; M = {2}; N = {0; 1}; E = {1; 2}; F = {0; 2}

Bài 5: Dùng các kí hiệu đoạn, khoảng, nửa khoảng, viết các tập hợp sau đây:

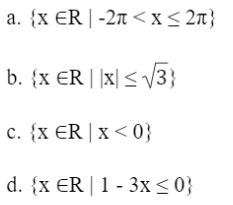
Đáp án chuẩn: