CHƯƠNG I. MỆNH ĐỀ VÀ TẬP HỢP

BÀI 2. TẬP HỢP

1. NHẮC LẠI VỀ TẬP HỢP

Ví dụ 1 (SGK – tr 16)

Chú ý:

Đôi khi, để ngắn gọn người ta dùng từ "tập" thay cho "tập hợp".

a∈S: phần tử a thuộc tập hợp S.

a∉S: phần tử a không thuộc tập hợp S.

Tập rỗng:

Mỗi tập hợp có thể không chứa phần tử nào, tập hợp như vậy gọi là tập rỗng, kí hiệu là ∅.

Chú ý: ∅≠{∅}  

Ví dụ 2 (SGK – tr16)

Các tập hợp số:

N là tập hợp các số tự nhiên;

Z là tập hợp các số nguyên;

Q là tập hợp các số hữu tỉ;

R là tập hợp các số thực.

Thực hành 1:

a) Tập hợp A là các số tự nhiên nhỏ hơn 5.

Ta có: 1∈A,4∈A.

+) B là tập hợp các nghiệm thực của phương trình x$^{2}$-3x+2=0.

Ta có: 1∈B,2∈B.

+) C là tập hợp các ước của 6.

Ta có: 1∈C,3∈BC.

b) 

Ví dụ:

1∈N,2∈N; -1∉N,-2∉N.

1∈Z,2∈Z; $\frac{1}{2}$∉Z,$\frac{2}{3}$∉Z.

$\frac{1}{2}$∈Q,$\frac{2}{3}$∈Q; $\sqrt{3}$∉Q;$\sqrt{2}$∉Q.

$\frac{1}{2}$∈R,$\frac{2}{3}$∈R; Kẹo ∉R; Cam ∉R.

Cách xác định tập hợp

Có thể mô tả một tập hợp bằng một trong hai cách sau:

Cách 1: Liệt kê các phần tử của tập hợp.

Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.

Chú ý: Khi liệt kê các phần tử của tập hợp:

a) Các phần tử có thể được viết theo thứ tự tùy ý.

b) Mỗi phần tử chỉ được liệt kê một lần.

c) Nếu quy tắc xác định các phần tử đủ rõ thì người dùng "...." mà không nhất thiết viết ra tất cả các phần tử của tập hợp.

Ví dụ: Tập hợp các số tự nhiên không quá 100 có thể được viết là {0; 1; 2; ....; 100}.

Ví dụ 3 (SGK – tr17)

Chú ý:

Có những tập hợp ta có thể đếm hết các phần tử của chúng đó là những tập hợp hữu hạn.

Nếu E là tập hợp hữu hạn thì số phần tử của nó được kí hiệu là n(E).

Ví dụ: n(∅)=0.

Thực hành 2:

a) A=-24;-12;-8;-6;-4;-3;-2;-1;1;2;3;4;6;8;12;24,

n(A)=16;

b) B={0;1;3;5},n(B)=4; 

c) C={0;5;10;15;20;25;30},n(C)=7; 

d) D=∅,n(D)=0.

Thực hành 3:

a) A={x∣x là số tự nhiên lẻ, x≤15};
b) B={xN∣x là bội của 5};
c) C={xR∣2x+5>0}.

2. TẬP CON VÀ HAI TẬP BẰNG NHAU 

HĐKP 1:

Các phần tử của tập hợp A đều thuộc tập hợp B.

Kết luận:

Cho hai tập hợp A và B. Nếu mọi phần tử của A đều là phần tử của B thì ta nói tập hợp A là tập con của tập hợp B và kí hiệu A⊂B (đọc là A chứa trong B), hoặc B⊃A (đọc là B chứa A).

Nhận xét:

+) A⊂A và ∅⊂A với mọi tập hợp A.

+) Nếu A không phải là tập con của B thì ta kí hiệu A⊄B.

+) Nếu A⊂B hoặc B⊂A thì ta nói A và B có quan hệ bao hàm.

Biểu đồ Ven:

Người ta thường minh họa một tập hợp bằng một hình phẳng được bao quanh bởi một đường kín, gọi là biểu đồ Ven.

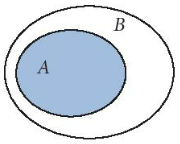
Chú ý: 

Mối quan hệ giữa các tập hợp số: N⊂Z⊂Q⊂R.

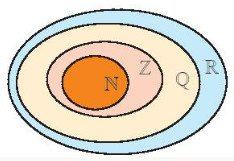
Kết luận:

Hai tập hợp A và B gọi là bằng nhau, kí hiệu A = B, nếu A⊂B và B⊂A.

Ví dụ 4 (SGK – tr19)

Thực hành 4: 

a) A=B;

b) C⊂D,C khác D;

c) E⊂F,E khác F.

Thực hành 5:

∅,{a},{b},{a;b}.

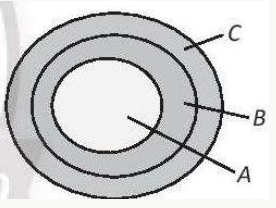
Vận dụng:

Khẳng định đúng. Từ biễu đồ Ven như hình bên, ta thấy miền biểu diễn A nằm trong miền biễu diễn C.

3. MỘT SỐ TẬP CON CỦA TẬP HỢP SỐ THỰC 

Thực hành 6:

a) (-2;3);
b) [1;10];
c) (-5;$\sqrt{3}$];
d) [$\pi $;4)
e) (-∞;$\frac{1}{4}$)

g) [$\frac{\pi}{2}$;+∞).