Slide bài giảng toán 7 chân trời bài 8: Tính chất ba đường cao của tam giác (2 tiết)

Tóm lược nội dung

CHƯƠNG 8: TAM GIÁC

BÀI 8: TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC

1. ĐƯỜNG CAO CỦA TAM GIÁC

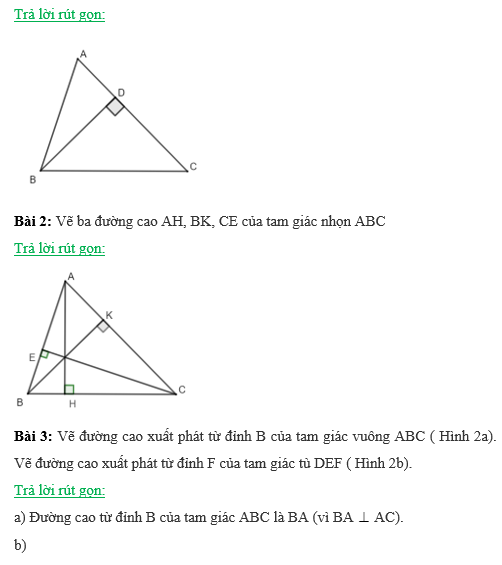
Bài 1: Em hãy vẽ một tam giác ABC trên giấy, sau đó dùng êke vẽ đoạn thẳng vuông góc từ đỉnh B đến cạnh đối diện AC của tam giác.

2. TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC

Bài 1: Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). Em hãy quan sát và cho biết các đường cao vừa vẽ có cùng đi qua một điểm hay không.

Trả lời rút gọn:

Cả 3 đường cao đều cùng đi qua một điểm.

Bài 2: Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6). Chứng minh rằng NS vuông góc ML.

Trả lời rút gọn:

Trong tam giác MNL  có :

LP ⊥ MN LP là đường cao của tam giác MNL.

MQ ⊥ LN MQ là đường cao của tam giác MNL.

LP giao với MQ tại S 

S là trực tâm của tam giác MNL

Vì 3 đường cao của tam giác cắt nhau tại 1 điểm.

NS ⊥ LM.

Bài 3: Cho tam giác ABC có ba đường cao AD, BE, CF đồng quy tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC.

Trả lời rút gọn:

+ Xét ∆ HBC có HD ⊥ BC

                         CE ⊥ BH

                         BF ⊥ CH

Tam giác HBC có 3 đường cao là HD, CE, BF.

Mà BF, DH, CE giao nhau tại A

A là trực tâm của ∆ HBC.

+ Xét ∆ HAB có HF ⊥ AB

                         AE ⊥ BH

                         BD ⊥ AH

Tam giác HAB có 3 đường cao là HF, AE, BD.

Mà BD, FH, AE giao nhau tại C

C là trực tâm của ∆ HAB.

+ Xét ∆ HAC có HE ⊥ AC

                          AF ⊥ CH

                         CD ⊥ AH

Tam giác HAC có 3 đường cao là HE, AF, CD.

AF, HE, CD giao nhau tại B

B là trực tâm của ∆ HAC.

BÀI TẬP

Bài 1: Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng  CH vuông góc với NB.

Trả lời rút gọn:

Xét tam giác CNB có :

BA ⊥ CA hay BA ⊥ CN BA là đường cao của tam giác CNB

HM ⊥ CB hay NM ⊥ CB NM là đường cao của tam giác CNB

NM giao với BA tại điểm H

H là trực tâm của tam giác CNB

CH ⊥ NB.

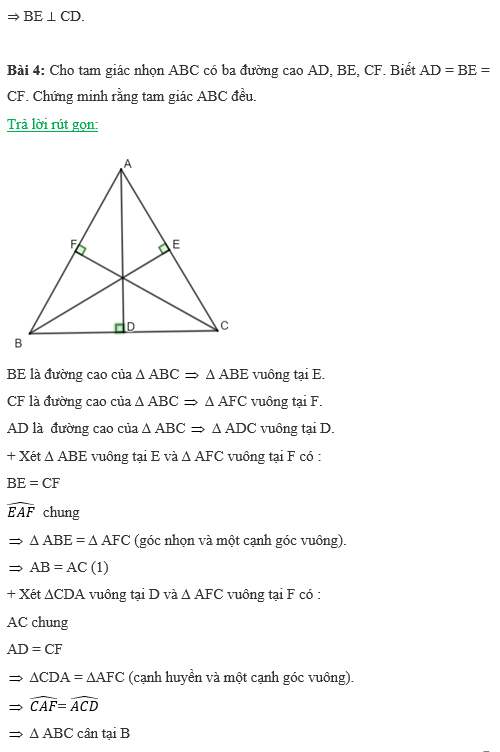
=> AB = BC (2)

Từ (1), (2) ta có : AB = AC = BC

=>  ∆ ABC đều.