Slide bài giảng toán 7 chân trời bài 4: Đường vuông góc và đường xiên (2 tiết)

Tóm lược nội dung

CHƯƠNG 8: TAM GIÁC

BÀI 4: ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN

1. QUAN HỆ GIỮA CẠNH VÀ GÓC TRONG MỘT TAM GIÁC

Bài 1: 

Cho tam giác ABC trong hình 1

- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ dài ba cạnh a, b, c

- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ lớn của ba góc A, B, C là các góc đối diện với ba cạnh a, b, c

- Nêu nhận xét của em về hai kết quả sắp xếp trên.
Trả lời rút gọn:

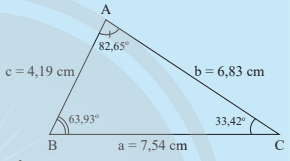
- Sắp xếp độ dài ba cạnh: c < a < b

- Sắp xếp độ lớn ba góc: < <

- Nhận xét : góc đối diện với cạnh lớn hơn là góc lớn hơn và ngược lại.

Bài 2: a) Sắp xếp theo thứ tự từ nhỏ đến lớn số đo các góc của tam giác PQR trong Hình 3a.

b) Sắp xếp theo thứ tự từ nhỏ đến lớn độ dài các cạnh của tam giác ABC trong hình 3b

Trả lời rút gọn:

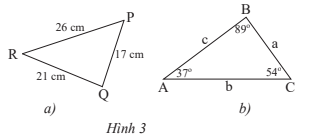
a) Xét  ∆ PQR ta có : PQ < RQ < PR

<  < .

b) Xét  ∆ ABC ta có:

  <  <  

BC < AB < AC.

Bài 3: a) Cho tam giác DEF có góc F là góc tù. Cạnh nào là cạnh có độ dài lớn nhất trong ba cạnh của tam giác DEF?

b) Cho tam giác ABC vuông tại A. Cạnh nào là cạnh có độ dài lớn nhất trong ba cạnh của tam giác ABC?

Trả lời rút gọn:

a) 

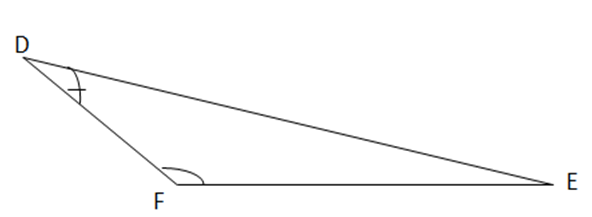
∆ DEF có góc F là góc tù 

góc F là lớn nhất 

DE là cạnh lớn nhất.

b) 

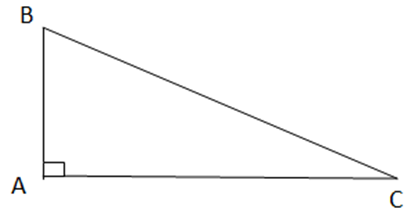
∆ ABC là tam giác vuông tại A

góc A là lớn nhất  

BC là cạnh có độ dài lớn nhất của ∆ABC.

2. ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN

Bài 1: Trong hình xe cần cẩu ờ hình 4, ta có đoạn thẳng MA biểu diễn trục cần cẩu , đoạn thẳng MH biểu diễn sợi cáp kéo dài ( từ đỉnh tay cẩu đến trên mặt đát ) , đường thẳng d biểu diễn mặt đất. Theo em, trong hai đoạn thẳng MA và MH, đoạn nào vuông góc với đường thẳng d ?

Trả lời rút gọn:

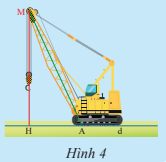
MH ⊥ d.

3. MỐI QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN

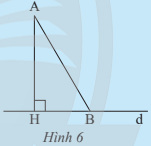
Bài 1: Quan sát tam giác vuông AHB ở hình 6.

a) Hãy cho biết trong hai góc AHB va ABH, góc nào lớn hơn.

b) Từ câu a, hãy giải thích vì sao AB > AH.

Trả lời rút gọn:

a) Góc > (vì là góc vuông; là góc nhọn)

b) Theo định lý về cạnh và góc đối diện trong một tam giác ta có : 

Xét ∆ AHB :   >  

AB > AH.

Bài 2: Trong hình 8, tìm đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BF. Trong số các đường này, đường nào ngắn nhất?

Trả lời rút gọn:

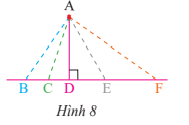
• Đường vuông góc : AD.
• Đường xiên : AB, AC, AE, AF.
• Đường ngắn nhất: AD.

Bài 3: Bạn Minh xuất phát từ điểm M bên hồ bơi (Hình 9). Bạn ấy muốn tìm đường ngắn nhất để bơi đến thành hồ đối diện. Theo em, bạn MInh phải đi theo đường bơi nào ?

Trả lời rút gọn:

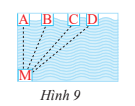
Theo hình vẽ, ta có MA ⊥ AD

MB, MC, MD là các đường xiên và MA là đường vuông góc.

MA là ngắn nhất

Minh nên đi theo đường MA.

BÀI TẬP

Bài 1: a) So sánh các góc của tam giác ABC có AB= 4 cm, BC = 7 cm, AC = 6 cm

b) So sánh các cạnh của tam giác ABC có = 50°, = 50°

Trả lời rút gọn:

a) 

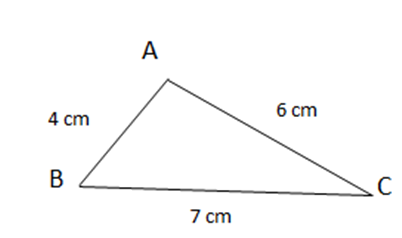
Xét ∆ABC ta có : AB < AC < BC

< <

b) 

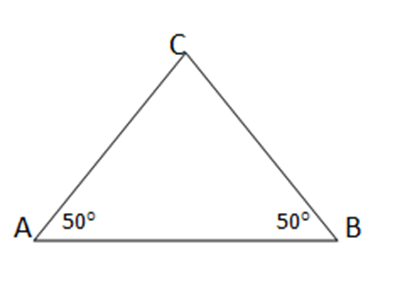
Ta có : = 50°, = 50°

  =   

 ∆ABC cân tại C

  =   180°- ( +  ) = 180° - 100° = 80°.

Xét ∆ABC ta có: > =

 AB > CA = CB.

Bài 2: Cho tam giác ABC có = 100°, = 40°

a) Tìm cạnh lớn nhất của tam giác ABC

b) Tam giác ABC là tam giác gì ? Vì sao ?

Trả lời rút gọn:

a) Một thanh nẹp gỗ có hai cạnh song song. Chiều rộng của thanh nẹp gỗ là khoảng cách giữa hai cạnh đó.

Hãy cho biết có phải chiều rộng của thanh nẹp gỗ là khoảng cách ngắn nhất từ một điểm trên cạnh này đến một điểm trên cạnh kia không.

b) Muốn đo chiều rộng của thanh nẹp, ta phải đặt thước như thế nào? Tại sao?

Trả lời rút gọn:

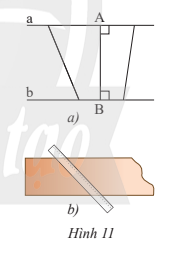
a) Chiều rộng của thanh nẹp gỗ là khoảng cách giữa hai cạnh đó.

Xét khoảng cách giữa hai cạnh đó là độ dài đoạn AB, mà AB là đoạn ngắn nhất trong các đường kẻ từ A đến cạnh còn lại (đường vuông góc luôn nhỏ hơn đường xiên).

Chiều rộng của thanh gỗ là khoảng cách ngắn nhất từ một điểm trên cạnh này đến một điêm trên cạnh kia.

b) Muốn đo chiều rộng của thanh nẹp ta đặt thước sao cho cạnh thước vuông góc với hai cạnh song song của thước gỗ.