Slide bài giảng toán 7 chân trời bài 5: Đường trung trực của một đoạn thẳng (2 tiết)

Tóm lược nội dung

CHƯƠNG 8: TAM GIÁC

BÀI 5: ĐƯỜNG TRUNG TRỰC CỦA MỘT ĐOẠN THẲNG

1. ĐƯỜNG TRUNG TRỰC CỦA MỘT ĐOẠN THẲNG

Bài 1: Lấy một mảnh giấy như trong hình 1a, gọi một mép cắt là đoạn thẳng AB. Sau đó gấp mảnh giấy sao cho điểm A trùng với điểm B ( hình 1b). Theo em nếp gấp xy có vuông góc với một đoạn AB tại trung điểm hay không?Tại sao ?

Trả lời rút gọn:

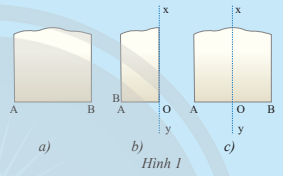
xy ⊥ AB tại trung điểm O.

Bài 2: Trong hình 4, hãy cho biết BD có là đường trung trực của đoạn thẳng AC hay không? Tại sao?

Trả lời rút gọn:

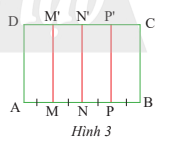
Có BC ⊥ AB

           MM' // BC  

MM' ⊥ AB hay MM' ⊥ AN

Tương tự ta có : NN' ⊥ AB , PP' ⊥ NB

AM = MN M là trung điểm của AN. Mà M'M ⊥ AN

MM' là đường trung trực của AN

NP = PB P là trung điểm của NB. Mà PP' ⊥ NB

PP' là đường trung trực của NB

 AM = MN = NP= PB AN= NB N là trung điểm của AB

NN' ⊥ AB. N là trung điểm của AB NN' là đường trung trực của AB.

Bài 3: Trong Hình 4, hãy cho biết BD có đường trung trực của đoạn thẳng AC hay không. Tại sao?

Trả lời rút gọn:

Xét ∆APD và ∆CPD có :

AD = CD

DP chung

= 

∆APD = ∆CPD (g.c.g)

=   

mà +  = 180°

2 = 180°

= 90°

DP ⊥ AP hay DP ⊥ AC

Mà P là trung điểm của AC

DP là đường trung trực của AC, hay DB là đường trung trực của AC.

2. TÍNH CHẤT CỦA ĐƯỜNG TRUNG TRỰC

Bài 1: Cho đoạn thẳng AB lấy O là trung điểm và d là đường trung trực. Lấy M tùy ý thuộc d ( Hình 5). Chứng minh rằng hai tam giác MOA và MOB bằng nhau, từ đó suy ra MA = MB

Trả lời rút gọn:

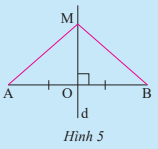
d là đường trung trực của AB tại điểm O 

∆MOA và ∆MOB là hai tam giác vuông tại O.

Xét ∆MOA và ∆MOB cùng vuông tại đỉnh O ta có:

MO chung

AO = OB ( O là trung điểm của AB)

∆MOA = ∆MOB (hai cạnh góc vuông)

MA = MB.

Bài 2: Trong hình 8, cho biết d là đường trung trực của đoạn thẳng AB, điểm M thuộc đường thẳng d, MA = x + 2 và MB = 7. Tính x.

Trả lời rút gọn:

M thuộc đường thẳng d mà d là đường trung trực của AB

MA = MB

x + 2 = 7 

 x = 7 - 2 = 5.

Vậy x = 5.

Bài 3: Dựng đường trung trực của đoạn thẳng AB bằng thước thẳng và compa theo hướng dẫn sau

• Lấy A làm tâm vẽ cung tròn bán kính lớn hơn 1/2 AB ( Hình 9a).
• Lấy B làm tâm vẽ cung tròn có bán kính bằng bán kính trên ( Hình 9b).
• Hai cung tròn này cắt nhau tại M và N ( Hình 9c). Dùng thước vẽ đường thẳng MN.

Hãy chứng minh đường thẳng MN chính là đường trung trực của đoạn thẳng AB

Trả lời rút gọn:

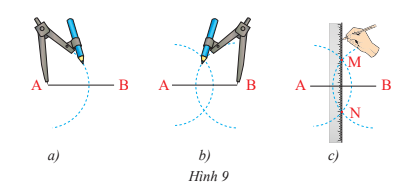
Ta có M thuộc 2 đường tròn tâm A và B

Mà bán kính đường tròn tâm A bằng với bán kính đường tròn tâm B

MA = MB

M cách đều hai đầu mút của đoạn thẳng B

M thuộc đường trung trực của AB

Tương tự ta có NA = NB

N cách đều hai đầu mút của đoạn thẳng AB

N thuộc đường trung trực của AB

MN là đường trung trực của AB.

BÀI TẬP

Bài 1: Hình 10 minh họa một tờ giấy có hình vẽ đường trung trực xy của đoạn thẳng AB mà hình ảnh điểm B bị nhòe mất. Hãy nêu cách xác định điểm B

Trả lời rút gọn:

AM là đường trung trực của đoạn thẳng BC

AB = AC, MB = MC

Ta có DB = DC = 8 cm

D cách đều 2 đầu mút của đoạn thẳng AB

D thuộc đường trung trực của AB

A, M, D cùng thuộc đường trung trực của AB

A, M, D thẳng hàng.

Bài 4: Quan sát hình 13, biết AB = AC, DB = DC. Chứng minh rằng M là trung điểm của BC

Trả lời rút gọn: 

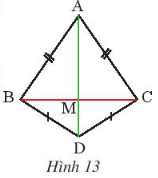
AB = AC A thuộc đường trung trực của BC

DB= DC D thuộc đường trung trực của BC

AD là đường trung trực của BC

Mà AD cắt BC tại M

M cũng thuộc đường trung trực AD

MB = MC

mà M thuộc BC

M là trung điểm của BC.      

Bài 5: Cho hai điểm M và N nằm trên đường trung trực d của đoạn thẳng EF

Chứng minh rằng ∆EMN = ∆FMN.

Trả lời rút gọn:

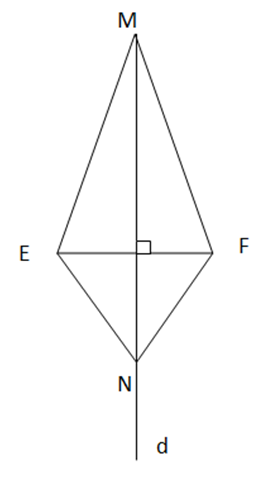
M, N thuộc đường trung trực d của đoạn thẳng EF

=> ME = MF, NE= NF

Xét ∆EMN và ∆FMN ta có:

ME = MF

NE = NF

MN chung 

∆EMN = ∆FMN (c.c.c)

Bài 6: Trên bản đồ quy hoạch một khu dân cư có một con đường d và hai điểm dân cư A và B ( Hình 14 ). Hãy tìm bên đường một địa điểm M để xây dựng một trạm y tế sao cho trạm y tế cách đều hai điểm dân cư.

Trả lời rút gọn:

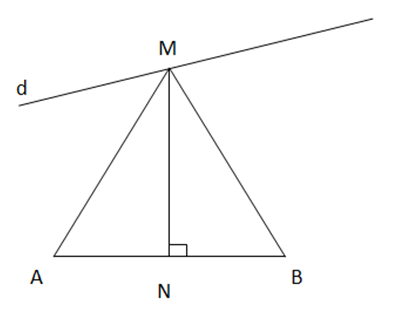
Gọi N là trung điểm của AB.

Qua N kẻ đường trung trực của đoạn thẳng AB, cắt đường thẳng d tại 1 điểm M.

=> M thuộc đường trung trực của AB

=> MA = MB

Vậy vị trí điểm M là nằm trên đường trung trực của đoạn thẳng AB.