Slide bài giảng toán 7 chân trời bài 3: Hai đường thẳng song song (4 tiết)

Tóm lược nội dung

CHƯƠNG 4: GÓC VÀ ĐƯỜNG THẲNG SONG SONG

BÀI 3: HAI ĐƯỜNG THẲNG SONG SONG

1. DẤU HIỆU NHẬN BIẾT HAI ĐƯỜNG THẲNG SONG SONG 

Bài 1: Quan sát Hình 3 và dự đoán các đường thẳng nào song song với nhau.

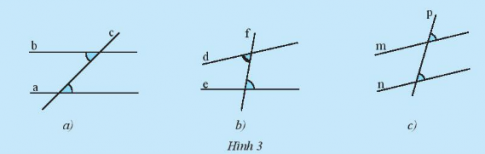
Trả lời rút gọn:

m//n và a//b là hai đường thẳng song song

Bài 2: Tìm các cặp đường thẳng song song trong Hình 5 và giải thích

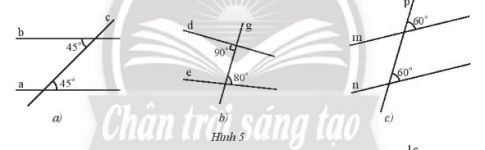
Trả lời rút gọn:

• Hình a: a // b vì đường thẳng c cắt 2 đường thẳng a, b và tạo thành một cặp góc so le trong bằng nhau
• Hình b: không có cặp đường thẳng nào song song vì đường thẳng g cắt 2 đường thẳng d, e và không tạo thành một cặp góc so le trong bằng nhau ( 90^o khác 80^o)
• Hình c: m // n vì đường thẳng p cắt 2 đường thẳng m, n và tạo thành một cặp góc đồng vị bằng nhau

Bài 3: Cho hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c tại A và B (Hình 6). Hãy chứng tỏ a//b.

Trả lời rút gọn:

Vì đường thẳng c cắt 2 đường thẳng a, b và tạo thành một cặp góc đồng vị bằng nhau (cùng bằng 90^o ) nên a // b (Dấu hiệu nhận biết 2 đường thẳng song song)

2. TIÊN ĐỀ EUCLID VỀ ĐƯỜNG THẲNG SONG SONG 

Bài 1: Cho điểm A nằm ngoài đường thẳng a, quan sát cách vẽ đường thẳng b đi qua A và song song với a ở Hình 8.

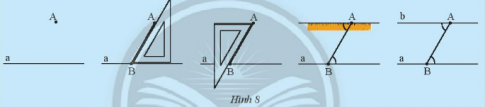
Trả lời rút gọn:

Có chỉ 1 đường thẳng b đi qua A và song song với đường thẳng a

Bài 2:

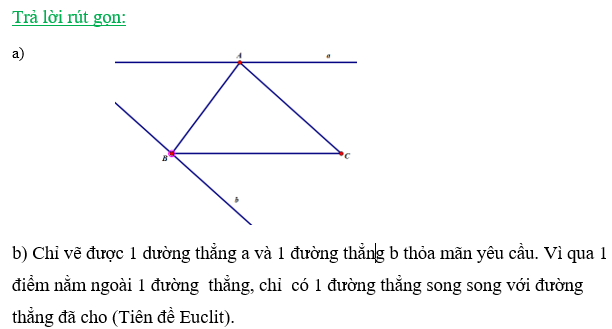
a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua A và song song với BC, vẽ đường thẳng b đi qua B và song song với AC.

b) Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?

3. TÍNH CHẤT CỦA HAI ĐƯỜNG THẲNG SONG SONG

Bài 1: Em hãy:

• Vẽ hai đường thẳng a và b song song với nhau
• Vẽ đường thẳng c cắt đường thẳng a và b lần lượt tại A và B.

a) Chọn và đo một cặp góc so le trong, so sánh cặp góc này.

b) Chọn và đo một cặp góc đồng vị, so sánh cặp góc này.

Trả lời rút gọn:

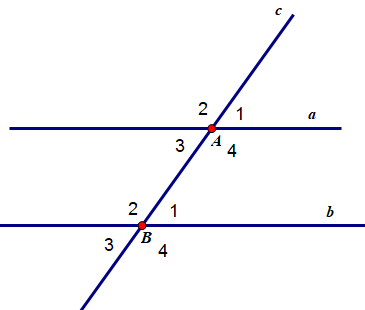
a) Một cặp góc so le trong là góc A₃ và góc B₁. Hai góc này cùng có số đo là 60^o nên chúng bằng nhau .

b) Một cặp góc đồng vị là góc A₁ và góc B . Hai góc này cùng có số đo là 60^o nên chúng bằng nhau.

Bài 2: Cho biết m // n và a // b. Tính số đo x,y,z và t của các góc trong hình 12.

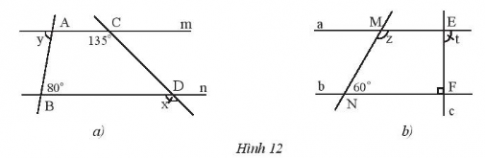
Trả lời rút gọn:

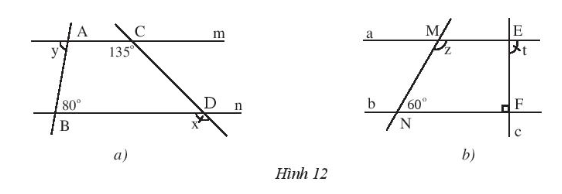
a) Vì m // n x = 135^o( 2 góc đồng vị) ; y = 80^o( 2 góc so le trong)

b) Vì a // b Góc M₁=60^o ( 2 góc đồng vị)

Có z + = 180^o

z = 180^o - = 180^o - 60^o = 120^o

a // b  t = = 90^o

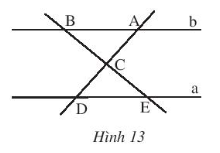
Bài 3: Tìm các cặp góc bằng nhau của hai tam giác ABC và DEC trong Hình 13, biết a // b.

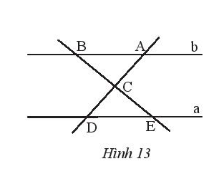
Trả lời rút gọn:

Vì a // b = ; = (2 góc so le trong)

= (2 góc đối đỉnh)

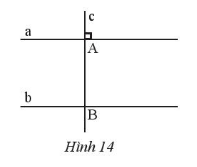
Bài 5: Cho hai đường thẳng a, b song song với nhau, đường thẳng c vuông góc với a tại A và cắt b tại B. Hãy giải thích tại sao đường thẳng c cũng vuông góc với b.

Trả lời rút gọn:

Vì a //b = (2 góc đối đỉnh)

mà = 90^o = 90^o

c vuông góc với b

BÀI TẬP

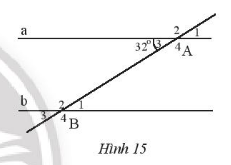
Bài 1: Trong Hình 15, cho biết a//b. Tìm số đo các góc đỉnh A và B.

Trả lời rút gọn:

Có : = = 32^o (2 góc đối đỉnh)

+ = 180^o (2 góc kề bù) = 180^o - = 180^o -32^o = 148^o

= = 148^o

Có: a//b = = 32^o (2 góc so le trong)

= = 148^o (2 góc so le trong)

= = 32^o (2 góc đối đỉnh)

= = 148^o (2 góc đối đỉnh)

Bài 2: Vẽ một đường thẳng cắt hai đường thẳng sao cho trong các góc tạo thành có một cặp góc so le trong bằng nhau. Đặt tên cho các góc đó.

a) Vì sao cặp góc so le trong còn lại cũng bằng nhau?

b) Vì sao các cặp góc đồng vị cũng bằng nhau?

Trả lời rút gọn:

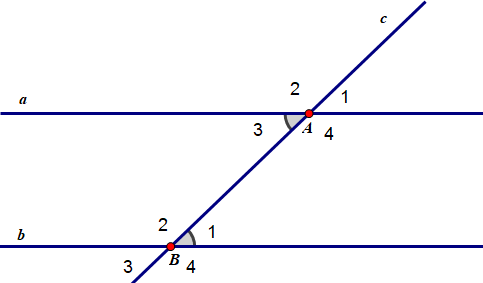
Vì đường thẳng c cắt hai đường thẳng a và b tạo thành một cặp góc so le trong ( giả sử góc A₃ và B₁) bằng nhau=> a // b ( Dấu hiệu nhận biết 2 đường thẳng song song) .

Vì a // b nên theo tính chất của 2 đường thẳng song song:

a) Các so le trong bằng nhau

b) Các góc đồng vị bằng nhau

Bài 3: Hãy nói các cách để kiểm tra hai đường thẳng song song mà em biết.

Trả lời rút gọn:

Cách 1: Kiểm tra 2 góc ở vị trí so le trong có bằng nhau không. Nếu bằng nhau thì 2 đường thẳng song song.

Cách 2: Kiểm tra 2 góc ở vị trí đồng vị có bằng nhau không. Nếu bằng nhau thì 2 đường thẳng song song.

Cách 3: Kiểm tra 2 đường thẳng có cùng song song với 1 đường thẳng thứ ba không. Nếu có thì 2 đường thẳng song song.

Cách 4: Kiểm tra 2 đường thẳng có cùng vuông góc với 1 đường thẳng thứ ba không. Nếu có thì 2 đường thẳng song song.

Bài 4: Cho Hình 16, biết a // b.

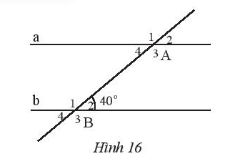
a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc

b) Tính số đo các góc  ,  ,

c) Tính số đo các góc ,

Trả lời rút gọn:

a) Góc ở vị trí so le trong với góc là:

Góc ở vị trí đồng vị với góc là:

b) Vì a //b 

=  = 40^o (2 góc so le trong)

  =  = 40^o (2 góc đồng vị)

Có: + = 180^o (hai góc kề bù)

= 180^o -  = 180^o - 40^o = 140^o

c) Có: + = 180^o (2 góc kề bù)

= 180^o - 40^o = 140^o 

Vì a // b = = 140^o (2 góc đồng vị)

Bài 5: Cho Hình 17, biết a // b.

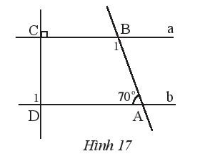
Tính số đo các góc và

Trả lời rút gọn:

a//b = = 70^o (2 góc so le trong)

Có: + = 180^o (2 góc kề bù)

= 180^o - = 180^o - 70^o = 110^o

a // b = = 90^o (2 góc đồng vị)

Có: + = 180^o

= 180^o - = 180^o - 90^o = 90^o 

Bài 6: Cho Hình 18, biết = 40, = 40 

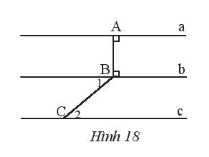
a) Đường thẳng a có song song với đường thẳng b không? Vì sao?

b) Đường thẳng b có song song với đường thẳng c không? Vì sao?

c) Đường thẳng a có song song với đường thẳng c không? Vì sao?

Trả lời rút gọn:

a) Vì a,b cùng vuông góc với đường thẳng AB nên a // b

b) Vì = .

Mà 2 góc này ở vị trí so le trong

b // c (Dấu hiệu nhận biết 2 đường thẳng song song)

c) Vì a // b, b //c a // c

Bài 7: Quan sát Hình 19 và cho biết:

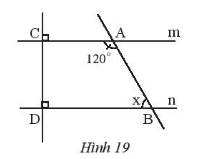
a) Vì sao m // n?

b) Số đo x của góc là bao nhiêu?