Slide bài giảng toán 7 cánh diều bài tập cuối chương VII (3 tiết)

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG VII

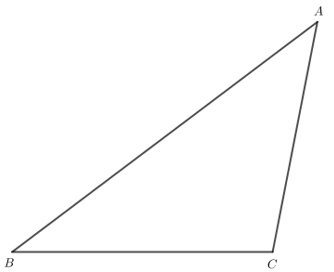
Bài 1: Cho tam giác ABC có . = 42°, = 37°.

a) Tính .

b) So sánh độ dài các cạnh AB, BC, CA.

Trả lời rút gọn:

a) Trong tam giác ABC:

b) Do nên

Do đó AC < BC < AB.

Bài 2: Tìm các số đo x, y trong Hình 140

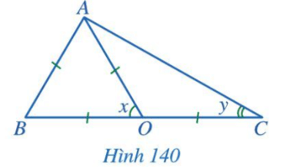
Trả lời rút gọn:

Tam giác ABO có OA = AB = BO nên tam giác ABO đều.

Do đó x = 60°.

Tam giác OAC có OA = OC nên tam giác OAC cân tại O.

Do đó .

Ta có: là góc ngoài tại đỉnh O của tam giác OAC nên hay x = 2y.

Do đó y = 30^o.

Bài 3: Bạn Hoa đánh dấu ba vị trí A, B, C trên một phần sơ đồ xe buýt ở Hà Nội năm 2021 và xem xe buýt có thể đi như thế nào giữa hai vị trí A và B. Đường thứ nhất đi từ A đến C và đi tiếp từ C đến B, đường thứ 2 đi từ B đến A. Theo em, đường nào đi dài hơn, vì sao?

Trả lời rút gọn:

Ba vị trí A, B, C tạo thành ba đỉnh của tam giác ABC.

Khi đó trong tam giác ABC: AB < AC + CB.

Vậy đường thứ nhất dài hơn đường thứ hai.

Bài 4: Cho hai tam giác ABC và MNP có: AB = MN, BC = NP, CA = PM. Gọi I và K lần lượt là trung điểm của BC và NP. Chứng minh AI = MK

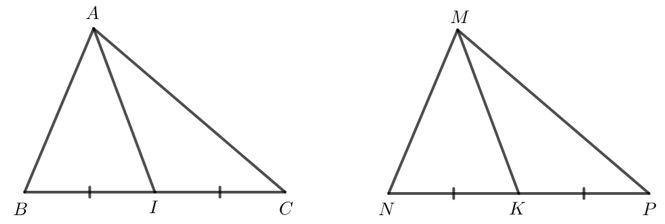
Trả lời rút gọn:

Xét ∆ABC và ∆MNP có:

AB = MN (theo giả thiết).

BC = NP (theo giả thiết).

CA = PM (theo giả thiết).

Do đó ∆ABC = ∆MNP (c - c - c).

Suy ra

Do I, K lần lượt là trung điểm của BC và NP mà BC = NP nên CI = PK.

+ Xét ∆ACI và ∆MPK có:

AC = MP (theo giả thiết).

CI = PK (chứng minh trên).

Do đó ∆ACI = ∆MPK (c - g - c).

Suy ra AI = MK (2 cạnh tương ứng).

Bài 5: Cho hình 142 có O là trung điểm của đoạn thẳng AB và O nằm giữa 2 điểm M, N. Chứng minh: 

a. Nếu OM = ON thì AM//BN

b. Nếu AM // BN thì OM = ON

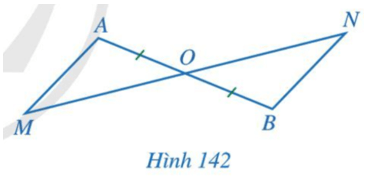
Trả lời rút gọn:

a) Xét ∆AOM và ∆BON có:

AO = BO (theo giả thiết).

OM = ON (theo giả thiết).

Do đó ∆AOM = ∆BON (c - g - c).

Suy ra

Mà hai góc này ở vị trí so le trong nên AM // BN.

b) Do AM // BN nên (2 góc so le trong).

Xét ∆AOM và ∆BON có:

AO = BO

(2 góc đối đỉnh).

Suy ra ∆AOM = ∆BON (g - c - g).

Suy ra OM = ON (2 cạnh tương ứng).

Bài 6: Cho tam giác ABC cân tại A có = 70⁰. Hai đường cao BD và CE cắt nhau tại H.

a. Tính số đo các góc còn lại của tam giác ABC

b. Chứng minh BD = CE

c. Chứng minh tia AH là tia phân giác của góc BAC

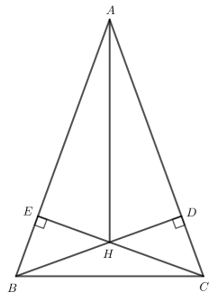
Trả lời rút gọn:

a) Tam giác ABC cân tại A nên AB = AC và .

Trong tam giác ABC:

b) Xét ∆ADB vuông tại D và ∆AEC vuông tại E có:

AB = AC (chứng minh trên).

chung

Do đó ∆ADB = ∆AEC (cạnh huyền - góc nhọn).

Suy ra BD = CE (2 cạnh tương ứng).

c) Do ∆ADB = ∆AEC (cạnh huyền - góc nhọn) nên AD = AE (2 cạnh tương ứng).

Xét ∆AEH vuông tại E và ∆ADH vuông tại D có:

AE = AD (chứng minh trên).

AH chung.

Do đó ∆AEH = ∆ADH (cạnh huyền - cạnh góc vuông).

Suy ra  (2 góc tương ứng).

Do đó AH là tia phân giác của góc BAC

Bài 7: Cho hai tam giác nhọn ABC và ECD, trong đó ba điểm B, C, D thẳng hàng. Hai đường cao BM và CN của tam giác ABC cắt nhau tại I, hai đường cao CP và DQ của tam giác ECD cắt nhau tại K. Chứng minh AI//EK.

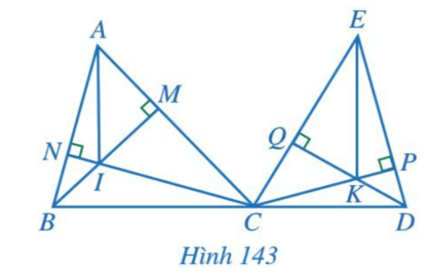
Trả lời rút gọn:

Tam giác ABC có hai đường cao BM và CN cắt nhau tại I nên I là trực tâm của tam giác ABC.

Suy ra AI ⊥ BC.

Tam giác ECD có hai đường cao CP và DQ cắt nhau tại K nên K là trực tâm của tam giác ECD.

Suy ra EK ⊥ CD.

Do B, C, D thẳng hàng nên AI ⊥ BC suy ra AI ⊥ BD.

EK ⊥ CD nên EK ⊥ BD.

Do đó AI // EK.