Slide bài giảng toán 7 cánh diều bài 5: Phép chia đa thức một biến (3 tiết)

Tóm lược nội dung

BÀI 5: PHÉP CHIA ĐA THỨC MỘT BIẾN

Khởi động

Câu hỏi: Trong quá trình biến đổi và tính toán những biểu thức đại số, nhiều khi ta phải thực hiện phép chia một đa thức (một biến) cho một đa thức (một biến) khác, chẳng hạn ta cần thực hiện phép chia sau: (x3+1):(x2−x+1)

Làm thế nào để thực hiện được phép chia hai đa thức một biến?

Trả lời rút gọn:

Muốn chia đa thức một biến A cho đa thức một biến (B ≠ 0) , trước hết ta phải sắp xếp các đa thức này theo lũy thừa giảm dần của cùng một biến và thực hiện phép chia như phép chia các số tự nhiên. Trong đó R=0 hoặc bậc của R thấp hơn bậc của B. Nếu R = 0 thì phép chia A cho B là phép chia hết.

I. Chia đơn thức cho đơn thức

Bài 1: Thực hiện phép tính:

a)

b)

c)

Trả lời rút gọn:

a)

b) .

c)

Bài 2: Tính:

Trả lời rút gọn:

II. Chia đa thức cho đơn thức

Bài 1: Ở Hình 6, diện tích các hình chữ nhật (I), (II) lần lượt là A = ac, B = bc. Biết MN = c

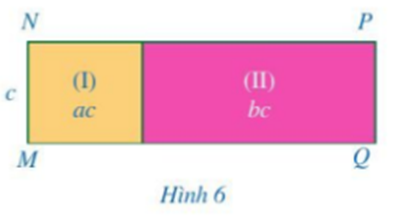
a) Tính NP.

b) So sánh: (A + B) : c và A : c + B : c. 

Trả lời rút gọn:

a) Độ dài cạnh kề với MN của hình chữ nhật (I) là A: c = ac: c = a.

Độ dài cạnh kề với PQ của hình chữ nhật (II) là B: c = bc: c = b.

Khi đó NP = a + b.

b) Diện tích MNPQ bằng tổng diện tích hai hình chữ nhật (I) và (II) bằng ac + bc.

Khi đó độ dài NP là thương trong phép chia diện tích hình chữ nhật MNPQ cho MN.

Hay NP = (ac + bc): c = (A + B): c.

Mà NP = a + b = A: c + B: c.

Do đó (A + B): c = A: c + B: c.

Bài 2: Cho đa thức P(x) = 4x²+3x và đơn thức Q(x) = 2x

a) Hãy chia từng đơn thức của biến x có trong đa thức P(x) cho đơn thức Q(x)

b) Hãy cộng các thương vừa tìm được

Trả lời rút gọn:

a) 

Bài 3: Tính:

Trả lời rút gọn:

= +

=

III. Chia đa thức một biến đã sắp xếp

Bài 1: Tính 

a) (x³ + 1): (x² - x + 1)

b) (8x³ - 6x² + 5) : (x² - x + 1)

Trả lời rút gọn:

a)

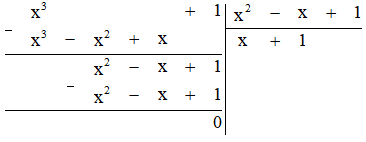
Vậy (x³ + 1): (x² - x + 1) = x + 1.

b)

Vậy 8x³ - 6x² + 5 = (8x + 2) . (x² - x + 1) + (-6x + 3).

IV. Bài tập

Bài 1: Tính :

Trả lời rút gọn:

x

Bài 2: Tính : 

Trả lời rút gọn:

Bài 3: Tính : 

a)

c)

d)

Trả lời rút gọn:

a) Thực hiện phép tính ta được:

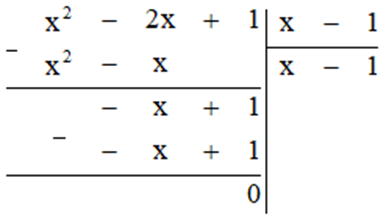
Vậy .

b) Thực hiện phép tính ta được:

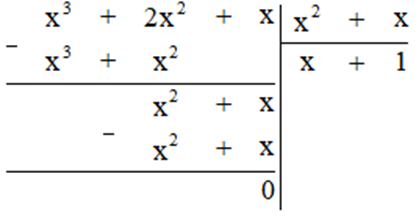
Vậy

c) Thực hiện phép tính ta được:

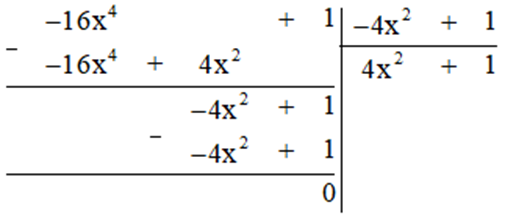
Vậy

d) Thực hiện phép tính ta được:

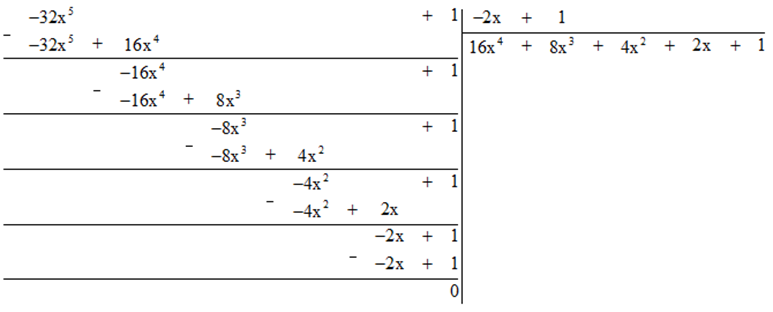
Vậy

Bài 4: Tính

a)

: (  -2x + x)

c) :

d) () : ( 3x + 1)

Trả lời rút gọn:

a) Thực hiện phép tính ta được:

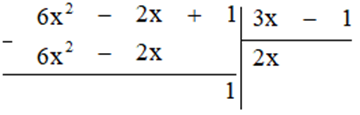
Vậy

b) Thực hiện phép tính ta được:

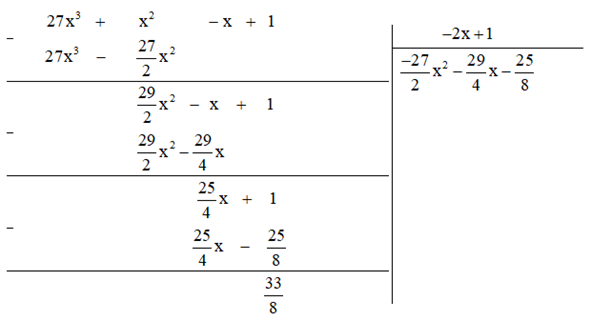
Vậy

c) Thực hiện phép tính ta được:

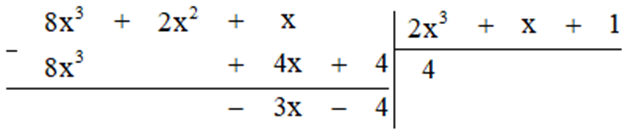
Vậy

d) Thực hiện phép tính ta được:

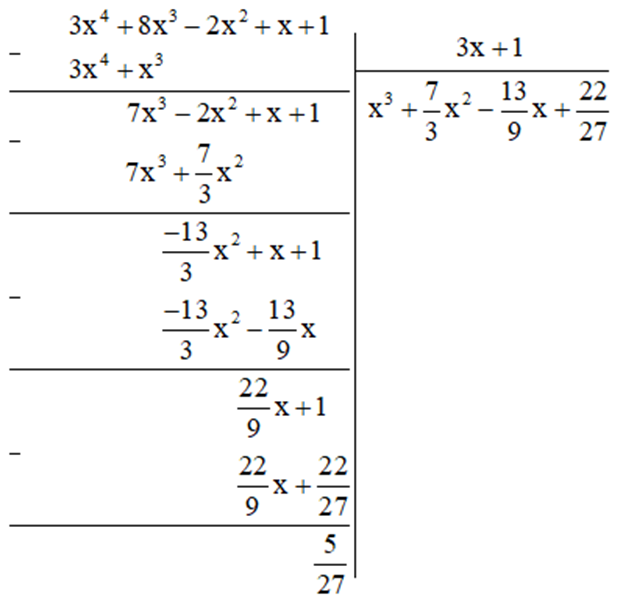
Vậy

Bài 5: Một công ty sau khi tăng giá 30 nghìn đồng mỗi sản phẩm so với giá ban đầu là 2x(nghìn đồng) thì có doanh thu là 6x²+170x+1200 (nghìn đồng). Tính số sản phẩm mà công ty đó đã bán được theo x.

Trả lời rút gọn:

Giá sản phẩm sau khi đã tăng giá là  (nghìn đồng).

Khi đó số sản phẩm mà công ty bán được là thương trong phép chia cho

Thực hiện phép tính ta được:

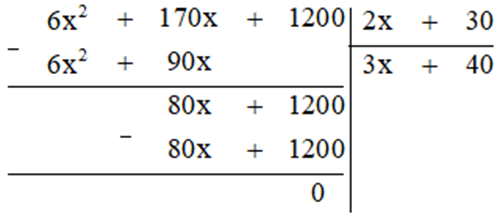
Vậy số sản phẩm mà công ty đó đã bán được là  sản phẩm.

Bài 6: Một hình hộp chữ nhật có thể tích là x³+6x²+11x+6(cm³). Biết đáy là hình chữ nhật có các kích thước là x+1 (cm) và x+2 (cm). Tính chiều cao của hình hộp chữ nhật đó theo x.

Trả lời rút gọn:

Diện tích đáy của hình hộp chữ nhật là:

Chiều cao của hình hộp chữ nhật là thương trong phép chia thể tích hình hộp chữ nhật cho diện tích đáy của hình hộp chữ nhật đó.

Thực hiện phép tính ta được:

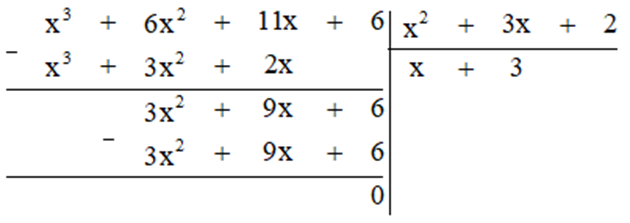
Vậy chiều cao của hình hộp chữ nhật đó là cm.