Slide bài giảng toán 7 cánh diều bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (3 tiết)

Tóm lược nội dung

BÀI 4: TRƯỜNG HỢP BẰNG NHAU THỨ NHẤT CỦA TAM GIÁC: 

CẠNH – CẠNH – CẠNH

Khởi động

Câu hỏi: Giá để đồ ở hình 33 gợi lên hình ảnh tam giác ABC và A'B'C' có: AB=A'B'; BC=B'C'; CA=C'A'. Tam giác ABC có bằng tam giác A'B'C' hay không?

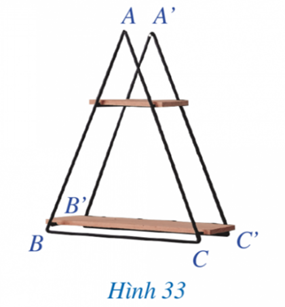
Trả lời rút gọn:

Tam giác ABC bằng tam giác A'B'C'.

I. Trường hợp bằng nhau cạnh – cạnh – cạnh (c.c.c)

Bài 1: Hai tam giác ở hình 37 có bằng nhau không? Vì sao?

Trả lời rút gọn:

Xét 2 tam giác ABC và ABD, ta có: 

AC = CD, BC = BD, AB chung 

Suy ra ΔABC = ΔABD (c.c.c)

II. Áp dụng vào trường hợp bằng nhau về cạnh huyền và cạnh góc vuông của tam giác vuông 

Bài 1: Cho hai tam giác vuông ABC và A'B'C' có: ==90⁰, AB=A'B'=3cm, BC=B'C'=5cm. So sánh độ dài các cạnh AC và A'C'

Trả lời rút gọn:

AC = A’C’

III. Bài tập

Bài 1: Cho Hình 42 có MN=QN; MP=QP. Chứng minh =

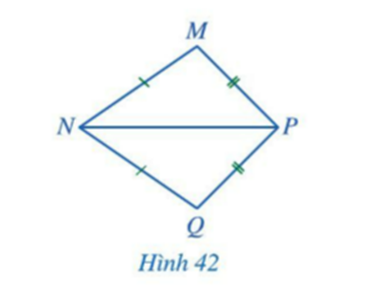
Trả lời rút gọn:

Vì MN = QN; MP = QP

=> ΔMNP = ΔQNP (c.c.c)

=> =

Bài 2: Cho Hình 43 có AB = AD, = 90⁰. Chứng minh

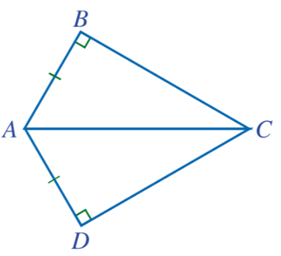
Trả lời rút gọn:

Xét hai tam giác vuông ABC và ADC, ta có: 

AB = AD (gt), AC là cạnh chung

Suy ra ΔABC = ΔADC (cạnh huyền – cạnh góc vuông)

=>

Bài 3: Cho hình 44 có AC = BD, = 90⁰. Chứng minh AD = BC.

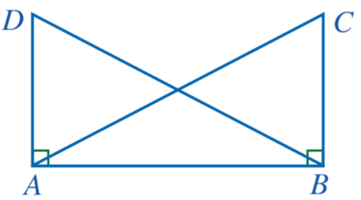
Trả lời rút gọn:

Xét hai tam giác vuông ABC và BAD, ta có: 

AC = BD (gt), AB là cạnh chung

Suy ra ΔABC = ΔBAD (cạnh huyền – cạnh góc vuông)

=> AD = BC

Bài 4: Cho hai tam giác ABC và MNP thỏa mãn: AB = MN, BC = NP, AC = MP, , . Tính số đo các góc còn lại của hai tam giác.

Trả lời rút gọn:

Xét hai tam giác ABC và MNP, ta có: 

AB = MN, BC = NP, AC = MP

Suy ra ΔABC=ΔMNP (c.c.c)

;