Slide bài giảng toán 7 cánh diều bài 6: Trường hợp bằng nhau thứ ba của tam giác - Góc – cạnh – góc (3 tiết)

Tóm lược nội dung

BÀI 6: TRƯỜNG HỢP BẰNG NHAU THỨ BA CỦA TAM GIÁC:

GÓC – CẠNH – GÓC

I. Trường hợp bằng nhau góc – cạnh – góc (g.c.g)

Bài 1: Cho hai tam giác ABC và A'B'C' thỏa mãn BC = B'C'=3cm, =60⁰, =50⁰, =70⁰. Hai tam giác ABC và A'B'C' có bằng nhau không? Vì sao?

Trả lời rút gọn:

Xét tam giác A’B’C’, ta có: 

(tổng 3 góc trong tam giác)

Xét 2 tam giác ABC và A'B'C' , ta có: 

BC = B’C’ (=3cm)

Suy ra ΔABC = ΔA’B’C’ (g.c.g)

Bài 2: Giải thích cho bài toán ở phần mở đầu

Có ba trạm quan sát A, B, C trong đó trạm quan sát C ở giữa hồ. Người ta muốn đo khoảng cách từ A và từ B đến C. Do không thể đo trực tiếp được các khoảng cách trên nên người ta làm như sau:

- Đo góc BAC được 60°, đo góc ABC được 45°;

- Kẻ tia Ax sao cho góc BAx = 60°, kẻ tia By sao cho ABy =45°,

xác định giao điểm D của hai tia đó;

- Đo khoảng cách AD và BD. Ta co AC = AD và BC = BD.

Trả lời rút gọn:

Xét 2 tam giác ABC và ABD' , ta có: 

AB là cạnh chung 

Suy ra ΔABC = ΔABD (g.c.g)

=> AC = AD, BC = BD 

II. Áp dụng vào trường hợp bằng nhau về cạnh góc vuông (hoặc cạnh huyền) và góc nhọn của tam giác vuông

III. Bài tập

Câu 1: Cho hai tam giác ABC và A'B'C' thỏa mãn: AB = A'B', ; . Hai tam giác ABC và A'B'C' có bằng nhau không? Vì sao?

Trả lời rút gọn:

Xét hai tam giác ABC và A’B’C’ , ta có: 

(cùng bằng )

AB = A’B’

Suy ra: ΔABC = ΔA’B’C’ (g.c.g)

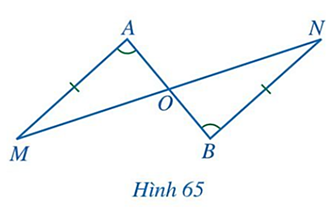
Bài 2: Cho Hình 65 có AM = BN, . Chứng minh: OA = OB, OM = ON

Trả lời rút gọn:

Chứng minh 

Có (gt)

Mà 2 góc nằm ở vị trí so le trong 

=> AM // BN => (2 góc so le trong)

Xét hai tam giác AMO và BNO , ta có: 

(gt)

AM = BN (gt)

(cmt) 

Suy ra: ΔAMO = ΔBNO (g.c.g)

=> OA = OB, OM = ON

Bài 3: Cho Hình 66 có , . Chứng minh MN = QP, MP = QN

Trả lời rút gọn:

Chứng minh

Xét hai tam giác vuông MNQ và QPM, ta có: 

(gt)

(gt)

MQ là cạnh chung 

Suy ra: Δ MNQ = Δ QPM (cạnh huyền – góc nhọn)

=> MN = QP, MP = QN

Bài 4: Cho hình 67 có = 90⁰, DH = CK, . Chứng minh AD = BC.

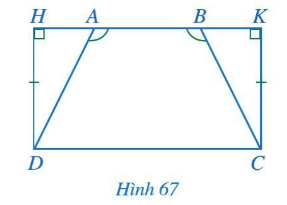
Trả lời rút gọn:

Vì => (góc bù nhau) 

Trong ΔHAD và ΔKBC có: 

= 90⁰

Mà  

=>

mà DH = CK

=> ΔHAD = ΔKBC (g.c.g)

=> AD = BC

Bài 5: Cho tam giác ADHBC có . Tia phân giác gõ BAC cắt cạnh BC tại điểm D.

a. Chứng minh

b. Kẻ tia Dx nằm trong ADC sao cho . Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh: ΔABD = ΔAED

Trả lời rút gọn:

a) Ta có: 

(tổng 3 góc trong ΔABD)

(tổng 3 góc trong ΔACD)

Mà (AD là phân giác góc BAC)

Lại có (gt)

Suy ra:

b) Xét hai tam giác ABD và AED, ta có: 

(AD là phân giác góc BAC)

AD là cạnh chung 

(gt )

Suy ra ΔABD = ΔAED (g.c.g)

=> AB = AE (2 cạnh tương ứng)

Mà AC = AE + EC