Slide bài giảng toán 7 cánh diều bài 13: Tính chất ba đường cao của tam giác (2 tiết)

Tóm lược nội dung

BÀI 13: TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC

Khởi động

Câu hỏi: Cho tam giác ABC. Gọi M, N, P lần lượt là hình chiếu của A, B, C trên các đường thẳng BC, CA, AB. Em có nhận xét gì về ba đường thẳng AM, BN, CP.

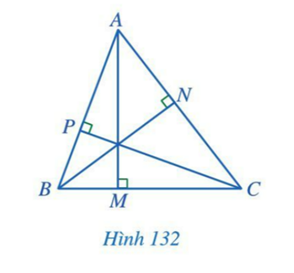
Trả lời rút gọn:

Ba đường thẳng AM, BN, CP cùng đi qua trực tâm của tam giác ABC.

I. Đường cao của tam giác

Bài 1: Cho tam giác ABC (Hình 133). Bằng cách sử dụng ê ke, vẽ hình chiếu M của điểm A trên đường thẳng BC.

Trả lời rút gọn:

Bài 2: Cho tam giác ABC vuông tại A. Hãy đọc tên đường cao đi qua B, đường cao đi qua C

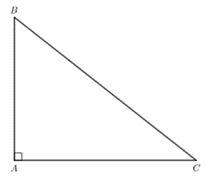
Trả lời rút gọn:

Đường cao đi qua B và vuông góc với AC là AB.

Đường cao đi qua C và vuông góc với AB là AC.

II. Tính chất ba đường cao của tam giác

Bài 1: Quan sát ba đường cao AM, BN, CP của tam giác ABC cho biết 3 đường cao đó có cùng đi qua 1 điểm hay không?

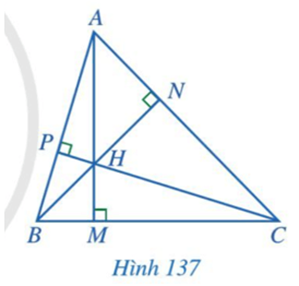
Trả lời rút gọn:

Ba đường cao AM, BN, CP của tam giác ABC cùng đi qua điểm H.

Bài 2: Cho tam giác đều ABC có trọng tâm là G. Chứng minh G cũng là trực tâm của tam giác ABC.

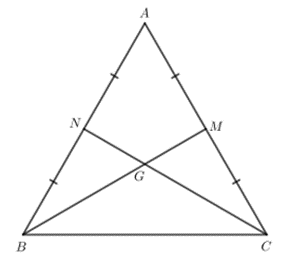
Trả lời rút gọn:

Gọi M, N theo thứ tự là trung điểm của AC và AB.

Do tam giác ABC đều nên AB = BC = CA và .

Do M là trung điểm của AC nên AM = CM.

Xét ∆BAM và ∆BCM có:

BA = BC (chứng minh trên).

AM = CM (chứng minh trên).

Do đó ∆BAM = ∆BCM (c - g - c).

Suy ra (2 góc tương ứng).

Mà nên

Do đó BM là đường cao của tam giác ABC.

Tương tự CN là đường cao của tam giác ABC.

Tam giác ABC có hai đường cao BM và CN cắt nhau tại G nên G là trực tâm của tam giác ABC.

Bài 3: Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều.

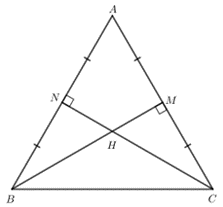
Trả lời rút gọn:

Gọi M, N lần lượt là trung điểm của AC và AB.

Do H là trực tâm của tam giác ABC nên CH ⊥ AB, BH ⊥ AC hay CN ⊥ AB, BM ⊥ AC.

Lại có H là trọng tâm của tam giác ABC nên BM, CN là các đường trung tuyến của tam giác ABC.

Khi đó BM vuông góc với AC tại trung điểm M của AC nên BM là đường trung trực của đoạn thẳng AC.

Do đó BA = BC (1).

Do CN vuông góc với AB tại trung điểm N của AB nên CN là đường trung trực của đoạn thẳng AB.

Do đó CA = CB (2).

Từ (1) và (2) suy ra AB = BC = CA nên tam giác ABC đều.

III. Bài tập

Bài 1: Tam giác ABC có H là trực tâm, H không trùng với đỉnh nào của tam giác. Nêu một tính chất của cặp đường thẳng

a. AH và BC

b. BH và CA

c. CH và AB

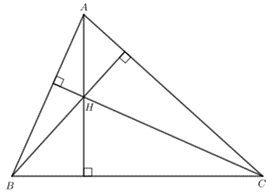
Trả lời rút gọn:

a) H là trực tâm của tam giác ABC nên AH ⊥ BC.

b) H là trực tâm của tam giác ABC nên BH ⊥ CA.

c) H là trực tâm của tam giác ABC nên CH ⊥ AB.

Bài 2: Cho tam giác ABC. Vẽ trực tâm H của tam giác ABC và nhận xét vị trí của nó trong các trường hợp sau:

a. Tam giác ABC nhọn

b. Tam giác ABC vuông tại A

c. Tam giác ABC có góc A tù

Trả lời rút gọn:

a) Ta có hình vẽ sau:

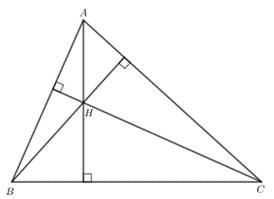
H nằm trong tam giác ABC.

b) Ta có hình vẽ sau:

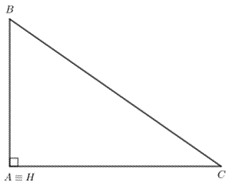
Xét tam giác ABC: AB ⊥ AC, AC ⊥ AB.

Do đó AB và AC là hai đường cao của tam giác ABC.

Mà AB cắt AC tại A nên A là trực tâm của tam giác ABC.

Do đó A trùng H.

c) Ta có hình vẽ sau:

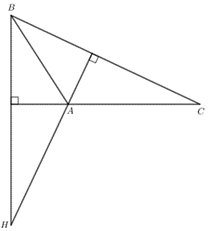
H nằm ngoài tam giác ABC.

Bài 3: Cho tam giác nhọn ABC và điểm D nằm trong tam giác. Chứng minh rằng nếu DA vuông góc với BC và DB vuông góc với CA thì DC vuông góc với AB.

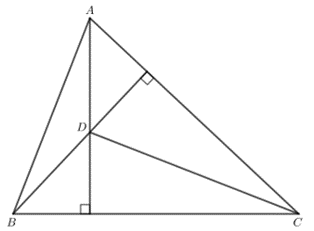
Trả lời rút gọn:

Tam giác ABC có DA ⊥ BC, DB ⊥ CA.

Mà DA cắt DB tại D nên D là trực tâm của tam giác ABC.

Do đó DC ⊥ AB.

Bài 4: Cho tam giác nhọn ABC. Hai đường cao BE và CF cắt nhau tại H, = 25^°. Tính và

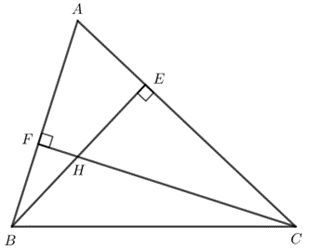
Trả lời rút gọn:

Xét ∆AFC vuông tại F có: (trong tam giác vuông, tổng hai góc nhọn bằng 90^o)

Suy ra hay

Xét ∆BEA vuông tại E có:

Suy ra hay .

Bài 5: Trong Hình 139, cho biết AB // CD, AD // BC; H, K lần lượt là trực tâm các tam giác ABC và ACD. Chứng minh AK // CH và AH // CK.

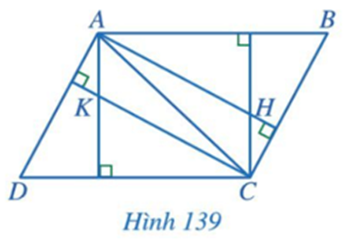
Trả lời rút gọn:

Do H là trực tâm của tam giác ABC nên CH ⊥ AB và AH ⊥ BC.

Do K là trực tâm của tam giác ADC nên AK ⊥ CD và CK ⊥ AD.

Do AB // CD nên AK ⊥ AB.

Mà CH ⊥ AB nên AK // CH.

Do AD // BC nên AH ⊥ AD.

Mà CK ⊥ AD nên AH // CK.

Bài 6: Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Chứng minh rằng:

a) Nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau;

b) Nếu tam giác ABC có hai điểm H, I trùng nhau thì tam giác ABC là tam giác đều.

Trả lời rút gọn:

a) Tam giác ABC đều:

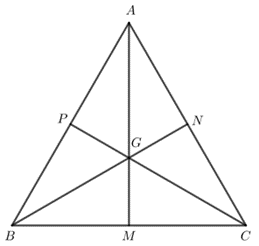
Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB.

Do tam giác ABC đều nên AB = BC = CA và

Do M là trung điểm của BC nên BM = CM.

Xét ∆AMB và ∆AMC có:

AB = AC (chứng minh trên).

BM = CM (chứng minh trên).

Do đó ∆AMB = ∆AMC (c - g - c).

Suy ra và (2 góc tương ứng).

Do  mà nên .

Khi đó AM vuông góc với BC tại trung điểm M của BC nên AM là đường trung trực của đoạn thẳng BC.

Lại có nên Am là đường phân giác của .

Chứng minh tương tự: 

+ BN là đường trung trực của đoạn thẳng CA và BN là đường phân giác của .

+ CP là đường trung trực của đoạn thẳng AB và CP là đường phân giác của 
.

Mà AM, BN, CP cắt nhau tại G nên G, H, I, O trùng nhau.

b) Tam giác ABC có H trùng I.

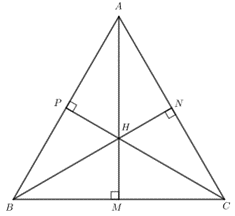
Gọi M, N, P lần lượt là chân đường cao kẻ từ H đến BC, CA, AB.

Khi đó HN ⊥ AC.

Mà H là trực tâm của ∆ABC nên BH ⊥ AC.

HN ⊥ AC, BH ⊥ AC nên B, H, N thẳng hàng.

+ Xét ∆APH vuông tại P và ∆CMH vuông tại M có:

HP = HM (theo giả thiết).

Do đó ∆APH = ∆CMH (góc nhọn - cạnh góc vuông).

Suy ra HA = HC (2 cạnh tương ứng).

+ Xét ∆HNA vuông tại N và ∆HNC vuông tại N có:

HN chung.

HA = HC (chứng minh trên).

Do đó ∆HNA = ∆HNC (2 cạnh góc vuông).

Suy ra AN = CN (2 cạnh tương ứng).

Khi đó N là trung điểm của AC.

HN ⊥ AC tại trung điểm N của AC nên HN là đường trung trực của đoạn thẳng AC.

Mà B, H, N thẳng hàng nên B thuộc đường trung trực của đoạn thẳng AC.

Do đó BA = BC.

Thực hiện tương tự, ta chứng minh được CA = CB.

Do đó AB = BC = CA.

Vậy tam giác ABC đều.