Slide bài giảng toán 7 cánh diều bài 12: Tính chất ba đường trung trực của tam giác (2 tiết)

Tóm lược nội dung

BÀI 12: TÍNH CHẤT BA ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC

Khởi động 

Câu hỏi: Làm thế nào để xác định được vị trí cách đều ba địa điểm được minh họa trong Hình 121?

Trả lời rút gọn:

Chúng ta cần xác định được giao điểm của 3 đường trung trực đi qua 3 địa điểm đó

I. Đường trung trực của tam giác

Bài 1: Cho tam giác ABC như Hình 122. Vẽ đường trung trực d của đoạn thẳng BC.

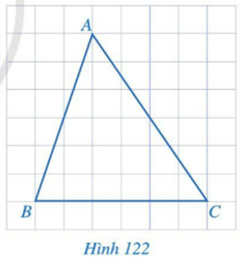
Trả lời rút gọn:

Bài 2: Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung trực của tam giác đó.

Trả lời rút gọn:

Xét tam giác ABD và tam giác ACD có: AB = AC (Vì tam giác ABC cân tại A) Góc B = Góc C (2 góc ở đáy của tam giác cân) Cạnh AD chung

=> Tam giác ABC = Tam giác ACD

=> BD = DC; Góc ADB = Góc ADB = 90 độ

=> AD vừa là đường phân giác vừa là đường trung trực của tam giác đó.

II. Tính chất ba đường trung trực của tam giác

Bài 1: Trong hình 127, điểm O có phải là giao điểm 3 đường trung trực của tam giác ABC không?

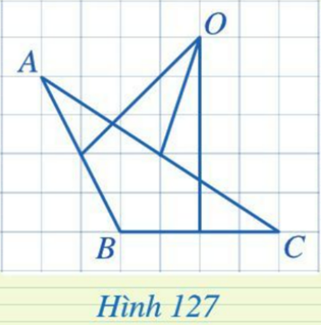
Trả lời rút gọn:

Trong hình 127, điểm O là giao điểm 3 đường trung trực của tam giác ABC.

Bài 2: Quan sát các đường trung trực của tam giác ABC (Hình 126) cho biết ba đường trung trực đó có cùng đi qua 1 điểm hay không?

Trả lời rút gọn:

Ba đường trung trực đó có cùng đi qua 1 điểm.

III. Bài tập

Bài 1: Cho tam giác ABC và điểm O thỏa mãn OA = OB = OC. Chứng minh rằng O là giao điểm 3 đường trung trực tam giác ABC

Trả lời rút gọn:

Vì OA = OB = OC

Nên O là tâm đường tròn ngoại tiếp ΔABC

Mà ΔABC đều

Nên O là giao điểm của ba tia phân giác của các góc A,B,C.

Bài 2: Cho tam giác ABC, vẽ điểm I cách đều ba đỉnh A, B, C trong mỗi trường hợp sau:

a. Tam giác ABC nhọn

b. Tam giác ABC vuông tại A

c. Tam giác ABC có góc A tù

Trả lời rút gọn:

HS tự thực hành

Bài 3: Tam giác ABC có ba đường trung tuyến cắt nhau tại G. Biết rằng điểm G cũng là giao điểm của ba đường trung trực trong tam giác ABC. Chứng minh tam giác ABC đều. 

Trả lời rút gọn:

Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB.

Do G vừa là trọng tâm của tam giác và P là trung điểm của AB nên C, G, P thẳng hàng.

Do G là giao điểm ba đường trung trực của tam giác nên G nằm trên đường trung trực của cạnh AB do đó C nằm trên đường trung trực của đoạn thẳng AB.

Suy ra CA = CB.

Thực hiện tương tự ta thu được BA = BC.

Do đó AB = BC = CA.

Tam giác ABC có AB = BC = CA nên tam giác ABC đều.

Bài 4: Tam giác ABC có ba đường phân giác cắt nhau tại I. Biết rằng I cũng là giao điểm ba đường trung trực của tam giác ABC. Chứng minh tam giác ABC đều.

Trả lời rút gọn:

Gọi M, N, P lần lượt là chân đường cao kẻ từ I đến BC, CA, AB.

Do I là giao điểm ba đường phân giác của tam giác ABC nên IM = IN = IP.

Do I là giao điểm ba đường trung trực của tam giác ABC nên I nằm trên đường trung trực của các cạnh BC, CA, AB.

Suy ra đường thẳng qua I, vuông góc với BC, CA, AB lần lượt là đường trung trực của các cạnh BC, CA, AB.

Do đó M, N, P lần lượt là đường trung trực của các cạnh BC, CA, AB.

Suy ra M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB.

Do AI là đường phân giác của nên =

Xét ∆PAI vuông tại P và ∆NAI vuông tại N có:

AI chung.

= (chứng minh trên).

Suy ra ∆PAI = ∆NAI (cạnh huyền - góc nhọn).

Do đó PA = NA (2 cạnh tương ứng).

Mà P là trung điểm của AB nên PA = BA; N là trung điểm của CA nên NA = CA.

Suy ra AB = CA.

Thực hiện tương tự ta thu được BA = BC.

Do đó AB = BC = CA.

Tam giác ABC có AB = BC = CA nên tam giác ABC đều.

Bài 5: Cho tam giác ABC. Đường trung trực của hai cạnh AB và AC cắt nhau tại điểm O nằm trong tam giác. M là trung điểm của BC. 

a) Chứng minh: OM ⊥ BC.

b) Chứng minh: =  

Trả lời rút gọn:

a) Tam giác ABC có O là giao điểm hai đường trung trực của đoạn thẳng AB và đoạn thẳng AC.

Mà ba đường trung trực trong tam giác đồng quy nên O nằm trên đường trung trực của đoạn thẳng BC.

Lại có M là trung điểm của BC nên OM là đường trung trực của đoạn thẳng BC.

Do đó OM ⊥ BC.

b) Do OM ⊥ BC nên ∆OMB và ∆OMC vuông tại M.

Xét ∆OMB vuông tại M và ∆OMC vuông tại M có:

OM chung.

MB = MC (theo giả thiết).

Do đó ∆OMB = ∆OMC (2 cạnh góc vuông).

Suy ra = (2 góc tương ứng).