Giải Hoạt động khám phá 4 trang 47 sgk Toán 8 tập 2 Chân trời

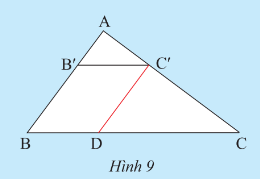
a) Xét tam giác ABC có B'C' // BC, nên theo định lí Thales ta có:

$\frac{AB'}{AB}=\frac{AC'}{AC}$ suy ra $\frac{2}{6}=\frac{AC'}{8}$, vậy AC' = $\frac{8}{3}$

b) Xét tam giác ABC có C'D // AB, nên theo định lí Thales ta có:

$\frac{BD}{BC}=\frac{AC'}{AC}$ suy ra $\frac{BD}{10}=\frac{\frac{8}{3}}{8}$, vậy $BD = \frac{10}{3}$

Xét tứ giác B'C'DB ta có: B'C'//BD, B'B // C'D nên B'C'DB là hình bình hành suy ra $B'C' = BD = \frac{10}{3}$

c) $\frac{AB'}{AB}=\frac{2}{6}=\frac{1}{3}$

$\frac{AC'}{AC}=\frac{\frac{8}{3}}{8}=\frac{1}{3}$

$\frac{B'C'}{BC}=\frac{\frac{10}{3}}{10}=\frac{1}{3}$

Vậy $\frac{AB'}{AB}=\frac{AC'}{AC}=\frac{B'C'}{BC}$