Giải bài tập 49 trang 79 SBT toán 8 tập 2 cánh diều:

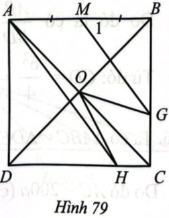
a) Ta có: $\widehat{CDB}=\widehat{CBD}$ = 45°. 

Mặt khác: $\widehat{DOH}+\widehat{BOG}$ = 180° - 45° = 135°;

$\widehat{BOG}+\widehat{BGO}$ = 180°- 45° = 135°.

=> $\widehat{DOH}=\widehat{BGO}$, do đó ΔHOD ᔕ ΔOGB.

b) Theo câu a, ta có ΔHOD ᔕ ΔOGB => $\frac{HD}{OB}=\frac{OD}{GB}$.

Đặt MB = a, AD = 2a 

=> HD.GB = OB.OD = a$\sqrt{2}$.a$\sqrt{2}$ = 2a$^{2}$ = AD.BM.

Vì HD.GB = AD.BM nên $\frac{HD}{AD}=\frac{BM}{BG}$ => ΔBMG ᔕ ΔDHA.

Do đó $\widehat{M_{1}}=\widehat{AHD}$, mà $\widehat{AHD}=\widehat{BAH}$ (hai góc so le trong, AB // CD).

Suy ra $\widehat{M_{1}}=\widehat{BAH}$. Mà $\widehat{M_{1}}$ và $\widehat{BAH}$ ở vị trí đồng vị nên AH // MG.