Giải bài tập 47 trang 79 SBT toán 8 tập 2 cánh diều:
Bài tập 47 trang 79 SBT toán 8 tập 2 cánh diều:
Cho tam giác ABC. Lấy E, F, P lần lượt thuộc AB, AC, BC sao cho tứ giác BEFP là hình bình hành (Hình 45). Biết diện tích tam giác AEF và CFP lần lượt bằng 16 cm$^{2}$ và 25 cm$^{2}$.
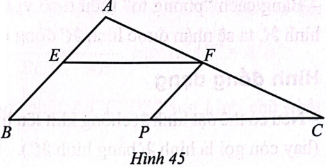
a) Hãy chỉ ra ba cặp tam giác đồng dạng.
b) Tính diện tích tam giác ABC.
a) Ba cặp tam giác đồng dạng là: ΔAEF ᔕ ΔABC, ΔFPC ᔕ ΔABC, ΔAEF ᔕ ΔFPC
b) Ta có ΔAEF ᔕ ΔABC, ΔFPC ᔕ ΔABC nên $\frac{S_{\Delta AEF}}{S_{\Delta ABC}}=\left (\frac{EF}{BC} \right )^{2}$
=> $\sqrt{\frac{S_{\Delta AEF}}{S_{\Delta ABC}}}=\frac{EF}{BC}$ (1).
Tương tự $\sqrt{\frac{S_{\Delta FPC}}{S_{\Delta ABC}}}=\frac{CP}{BC}$ (2).
Từ (1) và (2) => $\sqrt{\frac{S_{\Delta AEF}}{S_{\Delta ABC}}}+\sqrt{\frac{S_{\Delta FPC}}{S_{\Delta ABC}}}$ = $\frac{EF}{BC}+\frac{CP}{BC}=\frac{BP}{BC}+\frac{CP}{BC}$ = 1.
=> $\left (\sqrt{\frac{S_{\Delta AEF}}{S_{\Delta ABC}}}+\sqrt{\frac{S_{\Delta FPC}}{S_{\Delta ABC}}} \right )^{2}$ = 1
Hay $\left (\sqrt{\frac{16}{S_{\Delta ABC}}}+\sqrt{\frac{25}{S_{\Delta ABC}}} \right )^{2}$
=> $S_{\Delta ABC}$ = 81 cm$^{2}$.
Vậy diện tích tam giác ABC bằng 81 cm$^{2}$.

Bình luận