Giải bài tập 12 trang 63 SBT toán 8 tập 2 cánh diều:
Bài tập 12 trang 63 SBT toán 8 tập 2 cánh diều:
Một con dốc có độ nghiêng 30° so với mặt đất bằng phẳng. Đỉnh con dốc có độ cao CA là 500 m (Hình 17). Một người di chuyển trên dốc, khi đến vị trí K, cách đỉnh dốc 150 m thì người đó đang ở độ cao KH bằng bao nhiêu?
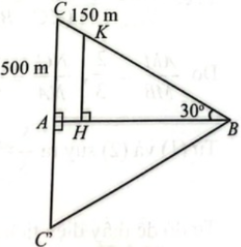
Trên tia đối của tia AC lấy C’ sao cho AC’ = AC.
Khi đó $\Delta $ACB = $\Delta $AC’B (c.g.c) nên BC = BC’.
Tam giác BCC’ có BC = BC’ và $\widehat{CBC’}$ = 60° nên là tam giác đều.
Suy ra CB = CC’ = 2. CA = 2.500 = 1 000 (m).
Do đó KB = CB – CK = 1 000 – 150 = 850 (m).
Do KH // CA nên theo hệ quả của định lí Thalès, ta có:
$\frac{KB}{CB}=\frac{KH}{CA}$ hay $\frac{850}{1000}=\frac{KH}{500}$.
=> KH = 425 m.
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận