Giải bài tập 11 trang 62 SBT toán 8 tập 2 cánh diều:
Bài tập 11 trang 62 SBT toán 8 tập 2 cánh diều:
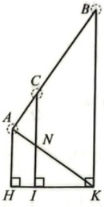
Ở một nhà máy, người ta dùng một băng chuyền để chuyển nguyên vật liệu. Ba vòng quay A, B, C của băng chuyền đặt cách mặt đất ở các độ cao lần lượt là AH = 5 (m), CI = 8 (m), BK = x (m) (Hình 16).

Tính x, biết AC = $\frac{2}{5}$CB.
Do AC = $\frac{2}{5}$CB nên AC = $\frac{2}{7}$AB.
Gọi N là giao điểm của AK và CI. Do CN // BK nên theo hệ quả của định lí Thalès, ta có:
$\frac{AC}{AB}=\frac{CN}{BK}$ hay $\frac{CN}{x}=\frac{2}{7}$
=> CN = $\frac{2}{7}$x (1).
Tương tự, do IN // AH, CN // BK nên $\frac{IN}{AH}=\frac{IK}{KH}=\frac{NK}{KA}=\frac{CB}{BA}=\frac{5}{7}$ hay $\frac{IN}{5}=\frac{5}{7}$
=> IN = 5.$\frac{5}{7}$ = $\frac{25}{7}$ (m) (2).
Từ (1) và (2) ta có: CI = CN + IN = $\frac{2}{7}x+\frac{25}{7}$.
Lại có CI = 8 (m) nên $\frac{2}{7}x+\frac{25}{7}=8$
=> $\frac{2}{7}x=\frac{31}{7}$
=> x = 15,5.
Vậy x = 15,5.

Bình luận