Đáp án đề số 2: Đề kiểm tra giữa kỳ I môn toán lớp 12
I.Đáp số
| 1: D | 2: A | 3: B | 4: A | 5: A | 6: A | 7: D | 8: A | 9: B | 10: B |
| 11: B | 12: B | 13: D | 14: C | 15: C | 16: B | 17: D | 18: A | 19: B | 20: C |
| 21: C | 22: C | 23: C | 24: D | 25: D | 26: C | 27: C | 28: D | 29: A | 30: C |
Câu 18:
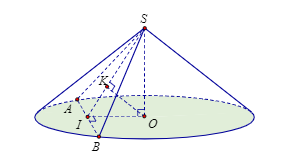
Ta có: AO = r = 25(cm); SO = h = 20(cm)
Tam giác SOI vuông tại O có OK vuông góc với SI, nên: $\frac{1}{OK^{2}}=\frac{1}{OI^{2}}+\frac{1}{OS^{2}}$
$\Rightarrow OI=15(cm)$
Có: $AB=2AI=\sqrt{25^{2}-15^{2}}=40(cm)$, $SI=\sqrt{SO^{2}+OI^{2}}=25(cm)$
Từ đó ta có: S_{\Delta SAB}=\frac{1}{2}.SI.AB=\frac{1}{2}.25.40=500(cm^{2})$.
Chọn A
Câu 20:
Ta có:
$x^{1+\frac{1}{2log_{4}x}}=x^{1+\frac{1}{log_{2}x}}=x^{1+log_{x}2}=x^{log_{x}x+log_{x}2}=x^{log_{x}2x}=2x$
$8^{\frac{1}{3log_{x^{2}}2}}=2^{3\frac{1}{3log_{x^{2}}2}}=2^{\frac{1}{log_{x^{2}}2}}=2^{log_{2}x^{2}}=x^{2}$
Khi đó: $f(x)=(x^{2}+2x+1)^{\frac{1}{2}}-1=[(x+1)^{2}]^{\frac{1}{2}}-1=x+1-1=x$
$\Rightarrow f(2017)=2017\Rightarrow f(f(2017))=f(2017)=2017$
Chọn C
Câu 24:
Ta có:
$P=(log_{a}b+log_{b}a+2)(log_{a}b-log_{ab}b)log_{b}a-1$
$=(log_{a}b+log_{b}a+2)(log_{a}b-log_{ab}b)log_{b}a-1$
$=(log_{a}b+log_{b}a+2)(log_{a}b-\frac{1}{log_{b}ab})log_{b}a-1$
$=log_{a}b+log_{b}a+2)(log_{a}b-\frac{1}{1+log_{b}a})log_{b}a-1$
Đặt $t=log_{b}a\Rightarrow P = (1+\frac{1}{t}+2)(\frac{1}{t})t-1=\frac{(t+1)^{2}}{t}.\frac{1}{t(t+1)}.t-1=\frac{t+1}{t}-1=\frac{1}{t}=log_{a}b$
Chọn D.
Câu 27:
Ta thấy các đáp án đều có tích xy nên ta sẽ đi tính xy theo a, b, c
Ta có:
$xy=log_{a}b^{2}.log_{b^{2}}\sqrt{c}=log_{a}\sqrt{c}=\frac{1}{2log_{a}c}$
$\Rightarrow log_{a}c=\frac{1}{2xy}$
Câu 30:
Ta đặt: $t=log_{9}p=log_{12}q=log_{16}(p+q)$.
$\Rightarrow \left\{\begin{matrix}p=9^{t}\\q=12^{t} \\p+q=16^{t} \end{matrix}\right.$
$\Rightarrow 9^{t}+12^{t}=16^{t}. (*)$
Chia hai vế của phương tình (*) cho $16^{t}$ ta được:
$\left ( \frac{9}{16} \right )^{t}+\left ( \frac{3}{4} \right )^{t}=1$
$\Rightarrow \left ( \frac{3}{4} \right )^{2t}+ \left ( \frac{12}{16} \right )^{t}=1$
$\Leftrightarrow( \frac{3}{4})^{t}=\frac{-1+\sqrt{5}}{2}$ do $\left ( \frac{3}{4} \right )^{t}>0$
$\Rightarrow A=\frac{p}{q}=\left ( \frac{3}{4} \right )^{t}=\frac{-1+\sqrt{5}}{2}$
Chọn C
Xem toàn bộ: Đề số 2: Đề kiểm tra giữa kỳ I môn toán lớp 12
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận