Đề 6: Luyện thi THPTQG môn Toán năm 2018
Đề 6: Luyện thi THPTQG môn Toán năm 2018. Đề gồm 50 câu hỏi, các em học sinh làm trong thời gian 90 phút. Khi làm xong, các em sẽ biết số điểm của mình và đáp án các câu hỏi. Hãy nhấn chữ bắt đầu ở phía dưới
Câu 1: Trong không gian chỉ có 5 loại khối đa diện đều
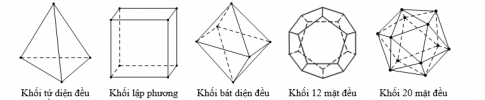
Mệnh đề nào sau đây là đúng?
A. Khối lập phương và khối bát diện đều có cùng số cạnh
- B. Khối mười hai mặt đều và khối hai mặt đều có cùng số đỉnh.
- C. Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng
- D. Mọi khối đa điện đều có số mặt là những số chia hết cho 4
Câu 2: Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;-1;1). Tìm tọa độ điểm M' là hình chiếu vuông góc của M trên mặt phẳng (Oxy)
A. M'(2;-1;0)
- B. M'(0;0;1)
- C. M'(-2;1;0)
- D. M'(2;1;-1)
Câu 3: Tập xác định của hàm số $y = (2-\sqrt{x-1})^{\sqrt{3}}$
- A. $D = (-\infty ; 5)$
B. D = [1;3)
- C. D = [1; 3)
- D. D = [1; $+\infty$)
Câu 4: Trong khoảng không gian với hệ tọa độ Oxyz, cho đường thẳng $\Delta $ đi qua điểm M(2;0;-1) và có véc tơ chỉ phương $\Delta $ = (4;-6;2). Phương trình tham số của $\Delta $ là:
- A. $\left\{\begin{matrix} & & & & \\ x = -2 + 4t & & & & \\ y = -6t & & & & \\ z = 1+2t & & & & \end{matrix}\right.$
- B. $\left\{\begin{matrix} & & & & \\ x = -2+2t & & & & \\ y = -3t & & & & \\ z = 1+t & & & & \end{matrix}\right.$
- C. $\left\{\begin{matrix} & & & & \\ x = 4 +2t & & & & \\ y = -3t & & & & \\ z = 1+t & & & & \end{matrix}\right.$
D. $\left\{\begin{matrix} & & & & \\ x = 2+2t & & & & \\ y = -3t & & & & \\ z = -1+t & & & & \end{matrix}\right.$
Câu 5: Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(1;2;-1), B(-3;4;3), C(3;1;-3). Số điểm D sao cho 4 điểm A,B,C,D là 4 đỉnh của một hình bình hành là:
- A. 3
- B. 1
- C. 2
D. 0
Câu 6: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;-2;1), B(1;4;3). Độ dài đoạn AB là
- A. 3
- B. $\sqrt{6}$
- C. $2\sqrt{3}$
D. $2\sqrt{13}$
Câu 7: Có bao nhiêu số chẵn gồm 3 chữ số khác nhau?
A. 328
- B. 405
- C. 360
- D. 500
Câu 8: Cho 2 số phức $z_{1} = 1 + 2i$, $z_{2} = 3 - i$ . Tìm số phức $z = \frac{z_{2}}{z_{1}}$:
- A. $z = \frac{1}{10} + \frac{7}{10}i$
- B. $z = \frac{1}{5} + \frac{7}{5}i$
C. $z = \frac{1}{5} - \frac{7}{5}i$
- D. $z = -\frac{1}{10} + \frac{7}{10}i$
Câu 8: F(x) là một nguyên hàm của hàm số f(x) = $3x^{2}+\frac{1}{2x +1}$. Biết F(0) = 0, F(1) = $a + \frac{b}{c}ln3$, trong đó a,b,c là các số nguyên dương và là phân số $\frac{b}{c}$ tối giản. Khi đó giá trị biểu thức a +b +c bằng
A. 4
- B. 3
- C. 12
- D. 9
Câu 10: Trong không gian với hệ tọa độ Ozyx, viết phương trình mặt cầu (S) có tâm I(0;1;-1) và tiếp xúc với mặt phẳng (P): 2x - y +2z -3 = 0
- A. $x^{2} +(y+1)^{2}+(z+1)^{2}= 4$
- B. $x^{2}+(y+1)^{2} +(z-1)^{2}=4$
C. $x^{2}+(y-1)^{2}+(z+1)^{2}=4$
- D. $x^{2}+(y-1)^{2}+(z+1)^{2}=2$
Câu 11: Thể tích khối tròn xoay sinh ra bởi phép quay trục hoành hình phẳng giới hạn bởi đồ thị hàm số $y = e^{\frac{x}{2}}$ , trục hoành, trục tung và đường thẳng x = 2 bằng:
- A. $\pi e^{2}$
B. $\pi (e^{2}-1)$
- C. $\pi (e-1)$
- D. $e^{2}-1$
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, $SA\perp (ABCD)$ , SC tạo với mặt phẳng đáy một góc $60^{\circ}$. Tính thể tích V của khối chóp đã cho.
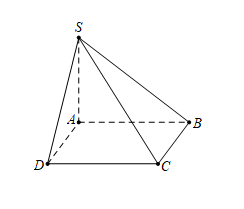
- A. $V = \frac{a^{3}\sqrt{6}}{6}$
- B. $V = \frac{a^{3}\sqrt{3}}{6}$
- C. $V = \frac{a^{3}\sqrt{6}}{3}$
D. $V = \frac{a^{3}\sqrt{3}}{3}$
Câu 13: Phương trình $4^{2x-4}$ có nghiệm là
A. x = 3
- B. x = 2
- C. x = 4
- D. x = 1
Câu 14: Cho tứ diện đều ABCD. Gọi $\varphi$ là góc giữa đường thẳng AB và mặt phẳng (BCD). Tính cos $\varphi$
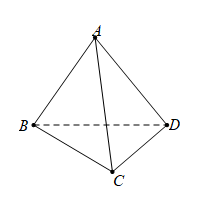
- A. $cos \varphi = \frac{1}{2}$
- B. cos $\varphi$ = 0
- C. $cos \varphi = \frac{\sqrt{2}}{3}$
D. $cos \varphi = \frac{\sqrt{3}}{3}$
Câu 15: Trong các mệnh đề sau đây, mệnh đề nào đúng?
- A. Số phức z = 2 - 3i có phần thực là 2 và phần ảo là -3i
B. Số phức z = 2 - 3i có phần thực là 2 và phần ảo là -3
- C. Số phức z = 2 - 3i có phần thực là 2 và phần ảo là 3i
- D. Số phức z = 2 - 3i có phần thực là 2 và phần ảo là 3
Câu 16: Hàm số nào sau đây đồng biến trên khoảng (-1;1)?
- A. $y = x^{2}$
B. $y = -x^{3}+3x$
- C. $y = \sqrt{1-x^{2}}$
- D. $y = \frac{x +1}{x}$
Câu 17: Cho hàm số y = f(x) có bảng biến thiên như hình vẽ
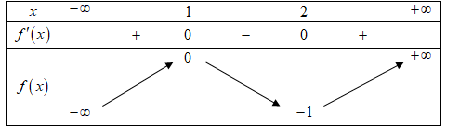
Hàm số có giá trị cực đại bằng
- A. 1
- B. 2
C. 0
- D. -1
Câu 18: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu. Các điểm A,B,C lần lượt là giao điểm (khác gốc tọa độ) của mặt cầu (S) và các trục tọa độ Ox, Oy, Oz. Phương trình mặt phẳng (ABC) là
- A. 6x -3y-2x-12 = 0
B. 6x +3y+2x-12 = 0
- C. 6x -3y-2x+12 = 0
- D. 6x -3y+2x-12 = 0
Câu 19: Khoảng cách giữa hai tiệm cận đứng của đồ thị hàm số $y = \frac{1}{x^{2}-2}$ bằng
- A. 2
- B. $\sqrt{2}$
C. $2\sqrt{2}$
- D. 4
Câu 20: Giá trị nhỏ nhất của hàm số $y= -x^{4}+4x^{2}-5$ trên [-2;3] bằng
- A. -5
B. -50
- C. -1
- D. -197
Câu 21: Diện tích của hình phẳng (H) được giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x = a, x = b $(a< b)$
- A. $S = \int_{a}^{c}f(x)dx+\int_{c}^{b}f(x)dx$
- B. $S = \frac{a}{b}f(x)dx$
- C. $S = \left | \int_{a}^{b}f(x)dx \right |$
D. $S = -\int_{a}^{c}f(x)dx + \int_{c}^{b}f(x)dx$
Câu 22: Đường cong hình bên là đồ thị của hàm số nào sau đây?

- A. $y = -x^{4}+4x^{2}$
- B. $y = x^{2}$
C. $y = 2x^{4}+x^{2}$
- D. $y = 3x^{4}-x^{2}+1$
Câu 23: Trong các khẳng định sau, khẳng định nào sai?
- A. $\left ( 1 - \frac{\sqrt{2}}{2} \right )^{2018} < \left ( 1 - \frac{\sqrt{2}}{2} \right )^{2017}$
- B. $2^{\sqrt{2}+1}> 2^{\sqrt{3}}$
- C. $\left ( \sqrt{2} -1\right )^{2017} > \left ( \sqrt{2} -1 \right )^{2018}$
D. $\left ( \sqrt{3} -1\right )^{2018}> \left ( \sqrt{3} -1\right )^{2017}$
Câu 24: Cho các số nguyên dương k,n $(k< n)$. Mệnh đề nào sau đây sai?
A. $C_{n}^{k} = \frac{n!}{(n-k)!}$
- B. $A_{n}^{k} = k!C_{n}^{k}$
- C. $C_{n}^{n-k} = C_{n}^{k}$
- D. $C_{n}^{k} + C_{n}^{k+1} = C_{n+1}^{k+1}$
Câu 25: Có bao nhiêu giá trị nguyên của m thuộc đoạn [-14, 15] sao cho đường thẳng y = mx + 3 cắt đồ thị của hàm số $y = \frac{2x + 1}{x -1}$ tại hai điểm phân biệt?
- A. 17
B. 16
- C. 20
- D. 15
Câu 26: Mệnh đề nào sau đây đúng?
A. Hàm số y = sin x đồng biến trên $\left ( 0; \frac{\pi }{2} \right )$
- B. Đồ thị hàm số y = sin x có tiệm cận ngang
- C. Hàm số y = sin x tuần hoàn với chu kì T = $\pi$
- D. Hàm số y = sin x là hàm số chẵn.
Câu 27: Cho hình lăng trụ tam giác đều ABC. A'B'C có tất cả các cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB và B'C'. Mặt phẳng (A'MN) cắt cạnh BC tại P. Thể tích khối đa diện MBP.A'B'N là

- A. $\frac{\sqrt{3}a^{3}}{24}$
B. $\frac{7\sqrt{3}a^{3}}{96}$
- C. $\frac{\sqrt{3}a^{3}}{12}$
- D. $\frac{7\sqrt{3}a^{3}}{32}$
Câu 28: Cho hàm số y = f(x) có bảng biến thiên như hình vẽ
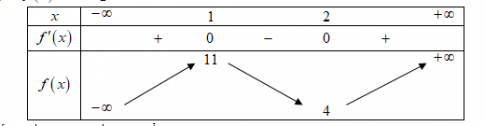
Đồ thị hàm số $y = \left | f(x)-2m \right |$ có 5 điểm cực trị khi và chỉ khi
- A. $m\in (4;11)$
- B. $m \in \left [ 2; \frac{11}{2} \right ]$
C. $m\in \left ( 2; \frac{11}{2} \right )$
- D. m = 3
Câu 29: Biết rằng phương trình $m\left ( \left | x \right |+\sqrt{1-x^{2}} +1\right )\leq 2\sqrt{x^{2}-x^{4}}+\sqrt{x^{2}}+\sqrt{1-x^{2}}+2$ có nghiệm khi và chỉ khi $m\in (-\infty ; a\sqrt{2}+b]$ với $a,b \in \mathbb{Z}$ . Tính giá trị của
- A. T = 0
B. T = 1
- C. T = 2
- D. T = 3
Câu 30: Cho hàm số $y = \frac{x +2}{x -2}$ có đồ thị là (C). Gọi I là giao điểm hai đường tiệm cận của (C). Tiếp tuyến của (C) cắt hai đường tiệm cận của (C) tại hai điểm A,B. Giá trị nhỏ nhất của chu vi đường tròn ngoại tiếp tam giác IAB bằng
- A. $2\pi$
- B. $8\pi$
C. $4\sqrt{2}\pi$
- D. $4\pi$
Câu 31: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có phương trình đường phân giác trong góc A là $\frac{x}{1} = \frac{y-6}{-4} = \frac{z-6}{-3}$. Biết rằng điểm M(0;5;3) thuộc đường thẳng AB và điểm N(1;1;0) thuộc đường thẳng AC. Véc tơ nào sau đây là véc tơ chỉ phương của đường thẳng AC?
- A. $\vec{u_{1}}= (1;2;3)$
- B. $\vec{u_{2}} = (0;-2;6)$
- C. $\vec{u_{3}} = (0;1;-3)$
D. $\vec{u_{4}} = (0;1;3)$
Câu 32: Cần phải làm cái cửa sổ mà phía trên là hình bán nguyệt, phía dưới là hình chữ nhật, có chu vi là a (mét) với a là chu vi hình bán nguyệt cộng với chu vi hình chữ nhật và trừ đi đường kính của hình bán nguyệt. Gọi d là đường kính của hình bán nguyệt. Hãy xác định d để diện tích của cửa sổ là lớn nhất.
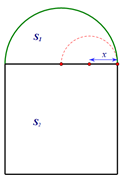
- A. $d = \frac{a}{4 +\pi }$
B. $d = \frac{2a}{4+\pi }$
- C. $d = \frac{a}{2 +\pi }$
- D. $d = \frac{2a}{2+\pi }$
Câu 33: Cho hình chóp S.ABCD có đáy ABC là tam giác vuông tại A, $\widehat{ABC} = 30^{\circ}$ , tam giác SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách h từ điểm C đến mặt phẳng (SAB)
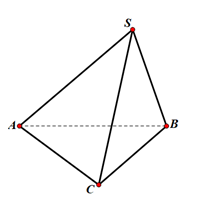
- A. $h = \frac{2a\sqrt{39}}{13}$
B. $h = \frac{a\sqrt{39}}{13}$
- C. $h = \frac{a\sqrt{39}}{26}$
- D. $h = \frac{a\sqrt{39}}{52}$
Câu 34: Trong mặt phẳng tọa độ Oxyz, gọi (H) là phần mặt phẳng chứa các điểm biểu diễn các số phức z thỏa mãn $\frac{z}{16}$ và $\frac{16}{z}$ có phần thực và phần ảo đều thuộc đoạn [0,1]. Tính diện tích S của (H)
- A. S = 256
- B. S = 64$\pi$
- C. S = 16(4-$\pi$)
D. S = 32(6-$\pi$)
Câu 35: Biết tích phân $\int_{0}^{ln6}\frac{e^{x}}{1+\sqrt{e^{x}+3}}dx = a-bln2 +cln3$ với a,b,c là các số nguyên dương. Tính giá trị của T = a + b + c
- A. T = 2
- B. T = 1
C. T = 0
- D. T = -1
Câu 36: Cho hàm số y = f(x) có đạo hàm liên tục trên đoạn $\left [ 0;\frac{\pi }{4} \right ]$ và $f\left ( \frac{\pi }{4} \right )=0$ . Biết rằng ta có điều kiện $\int_{0}^{\frac{\pi }{4}}f^{2}(x)dx = \frac{\pi }{8}$, $\int_{0}^{\frac{\pi }{4}}f'(x)sin2xdx = -\frac{\pi }{4}$. Tích phân $\int_{0}^{\frac{\pi }{8}}f(2x)dx)$
- A. $I = \frac{1}{2}$
B. $I = \frac{1}{2}$
- C. I = 2
- D. I = 1
Câu 37: Tìm tập hợp tất cả các giá trị thực của m để phương trình $1+log_{5}(x^{2}+1) = log_{5}(mx^{2}+4x +m)$ có hai nghiệm phân biệt?
A. $m\in (3;7)\setminus \left \{ 5 \right \}$
- B. $m \in (3;7)$
- C. $m\in \mathbb{R}\setminus \left \{ 5 \right \}$
- D. $m\in \mathbb{R}$
Câu 38: Biết $\int_{e}^{e^{4}}f(lnx)\frac{1}{x}dx=4$ . Tính tích phân $I = \int_{1}^{4}f(x)dx$
- A. I = 8
- B. I = 16
- C. I = 2
D. I = 4
Câu 39: Cho khai triển $(1-4x)^{18} = a_{0} + a_{1}x + a^{2}x +...+a^{18}x$. Giá trị của $a_{0}$ bằng:
A. -52224
- B. 52224
- C. 2448
- D. -2448
Câu 40: Cho các số phức $z_{1}$, $z_{2}$ thỏa mãn $\left | z_{1} \right |= 6$, $\left | z_{2} \right |= 2$. Gọi M,N lần lượt là điểm biểu diễn các số phức $z_{1}$, $z_{2}$. Biết rằng $\widehat{MON}= 60^{\circ}$. Tính giá trị của T = $\left | z_{1}^{2}+9z_{2}^{2} \right |$
- A. T = $36\sqrt{2}$
- B. T = $24\sqrt{3}$
C. T = $36\sqrt{3}$
- D. T = 18
Câu 41: Gọi S là tập hợp tất cả các giá trị thực của m sao cho giá trị lớn nhất của hàm số $y = \left | \frac{x^{2}+mx+m}{x+1} \right |$ trên đoạn [1;2] bằng 2. Số phần tử của tập hợp S là:
- A. 3
- B. 1
- C. 4
D. 2
Câu 42: Cho hàm số y = f(x) liên tục trên. Biết rằng hàm số y = f'(x) có đồ thị như hình bên. Hỏi hàm số $y = f(x^{2}-5)$ nghịch biến trên khoảng nào sau đây?
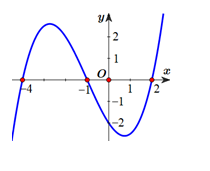
- A. (-1;0)
- B. (1;2)
- C. (-1;1)
D. (0;1)
Câu 43: Ông A muốn sau 5 năm có 1.000.000.000 đồng để mua ô tô Camry. Hỏi ông A phải gửi ngân hàng mỗi tháng với số tiền gần nhất với số tiền nào sau đây? Biết rằng lãi suất hàng tháng là 0.5% tiền lãi sinh ra hàng tháng được nhập vào tiền vốn ban đầu, số tiền gửi hàng tháng là như nhau:
- A. 14.261.000 đồng
- B. 14.260.500 đồng
C. 14.261.500 đồng
- D. 14.260.000 đồng
Câu 44: Cho dãy số $(u_{n})$ xác định bởi $\left\{\begin{matrix} & & & \\ u_{1} = 1 & & & \\ u_{n+1}=u_{n}+n^{3} & & & \end{matrix}\right.$, $\forall n\in \mathbb{N}*$. Tìm số nguyên dương n nhỏ nhất sao cho $\sqrt{u_{n}-1}\geq 2039190$ ?
- A. n = 2017
B. n = 2020
- C. n = 2018
- D. n = 2019
Câu 45: Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi và góc tạo bởi các mặt phẳng (SAB), (SBC), (SCD), (SDA) với mặt đáy lần lượt là $90^{\circ}$, $60^{\circ}$, $60^{\circ}$, $60^{\circ}$. Biết rằng tam giác SAB vuông cân tại S, AB = a và chu vi tứ giác ABCD là 9a. Tính thể tích V của khối chóp S.ABCD?
- A. $V = \frac{a^{3}\sqrt{3}}{4}$
- B. $V = a^{3}\sqrt{3}$
- C. $V = \frac{2a^{3}\sqrt{3}}{9}$
D. $V = \frac{a^{3}\sqrt{3}}{9}$
Câu 46: Cho hàm số y = f(x) liên tục trên đoạn [1;4] và thỏa mãn $f(x) = \frac{f(2\sqrt{x}-1)}{\sqrt{x}}+\frac{lnx}{x}$. Tính tích phân của $I = \int_{3}^{4}f(x)dx$
A. $I = 2ln^{2}2$
- B. $I = 2ln2$
- C. $I = 3 + 2ln^{2}2$
- D. $I = ln^{2}2$
Câu 47: Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;-3) và mặt phẳng (P): 2x +2y - z + 9 = 0. Đường thẳng đi qua A và vuông góc với mặt phẳng (Q): 3x + 4y - 4z + 5 = 0 cắt mặt phẳng (P) tại B. Điểm M nằm trong mặt phẳng (P) sao cho M luôn nhìn đoạn AB dưới một góc vuông và độ dài MB lớn nhất. Độ dài MB là:
A. $MB = \sqrt{5}$
- B. $MB = \frac{\sqrt{5}}{2}$
- C. $MB = \frac{\sqrt{41}}{2}$
- D. $MB = \sqrt{41}$
Câu 48: Cho lăng trụ ABCD.A'B'C'D' là hình chữ nhật, AB = a, AD =$a\sqrt{3}$ . Hình chiếu vuông góc của điểm A' trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B' đến mặt phẳng (A'BD) là:
- A. $\frac{a\sqrt{3}}{3}$
- B. $\frac{a\sqrt{3}}{4}$
C. $\frac{a\sqrt{3}}{2}$
- D. $\frac{a\sqrt{3}}{6}$
Câu 49: Giải bóng chuyền VTV Cup gồm 12 đội tham dự trong đó có 9 đội bóng nước ngoài, 3 đội bóng của Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành 3 bảng A,B,C mỗi bảng có 4 đội. Tính xác suất để 3 đội Việt Nam ở 3 bảng khác nhau:
A. $\frac{16}{55}$
- B. $\frac{133}{165}$
- C. $\frac{32}{165}$
- D. $\frac{39}{65}$
Câu 50: Cho hình nón đỉnh S, có đáy là hình tròn nội tiếp tam giác ABC. Biết rằng AB = BC = 10a, AC = 12a, góc tạo bởi mặt phẳng (SAB) và (ABC) bằng $45^{\circ}$. Tính thể tích V của khối nón đã cho.
A. $V = 9\pi a^{3}$
- B. $V = 12\pi a^{3}$
- C. $V = 27\pi a^{3}$
- D. $V = 3\pi a^{3}$
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận