Đề số 2: Đề kiểm tra giữa kỳ I môn toán lớp 12
Thầy cô và học sinh có thể tham khảo đề số 2: kiểm tra giữa kỳ I môn toán lớp 12 do Tech12h.com biên soạn. Đề thi sẽ giúp các em học sinh ôn luyện chuẩn bị cho kỳ thi giữa kỳ I sắp tới. Đề gồm 30 câu trắc nghiệm. Thời gian làm bài trong 60 phút!
Đề số 2: Đề kiểm tra giữa kỳ I môn toán lớp 12 (thời gian: 60 phút)
Câu 1: Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình lập phương là đa diện lồi
B. Tứ diện là đa diện lồi
C. Hình hộp là đa diện lồi
D. Hình tạo bởi hai tứ diện đều ghép với nhau là một hình đa diện lồi
Câu 2: Đường cong trong hình dưới là đồ thị hàm số nào sau đây?
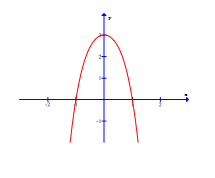
A. $-x^{4}-2x^{2}+3$
B. $x^{4}-2x^{2}+2$
C. $x^{2}-2x+2$
D. $y=x^{6}+x^{2}+9$
Câu 3: Giải phương trình $3^{x}-8.3^{\frac{x}{2}}+7=0$
A. x=0 hoặc $x=\log_{8}^{7}$
B. x=0 hoặc $x=\log_{8}^{49}$
C. x=0 hoặc $x=\frac{1}{2}\log_{8}^{7}$
D. x=1 hoặc $x=\log_{8}^{49}$
Câu 4: Cho hình lập phương có cạnh đáy bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S1 là diện tích 6 mặt của hình lập phương, S2 là diện tích xung quanh của hình trụ. Tính tỉ số giữa S2 và S1.
A. $\frac{\pi}{6}$
B. $\frac{\pi}{2}$
C.$\frac{1}{2}$
D.$ \pi $
Câu 5: Tập hợp nghiệm của bất phương trình $log_{\frac{1}{2}}(x^{2}-3x+2)\geq -1$ là:
A. $[0 ;1)\cup (2;3]$B
C. (0;3]
D. $(-\infty ;0]\cup [3;+\infty )$
Câu 6: Tập xác định của hàm số $ln\left (\sqrt{x^{2}+9x-1} \right )$ là :
A. $(-\infty ;10)\cup (1;+\infty )$
B. (-10;1)
C. $(-\infty ;10)$
D. $(1;+\infty )$
Câu 7: Cho $log_{2}5=m$,$log_{8}5=n$. Khi đó$log_{6}5$ được tính theo m, n là:
A. $\frac{2}{m+n}$
B. $\frac{m-n}{m+n}$
C. $m^{2}+2n$
D. $\frac{m.n}{m+n}$
Câu 8: Một tứ diện đều cạnh a có một đỉnh trùng với đỉnh của hình nón tròn xoay còn ba đỉnh còn lại của tứ diện nằm trên đường tròn đáy của hình nón. Diện tích xung quanh của hình nón tròn xoay là một trong các kết quả sau:
A. $\frac{1}{3}\pi.a^{2}\sqrt{3}$
B. $\pi.a^{2}\frac{\sqrt{2}}{3}$
C. $\pi.a^{2}\sqrt{2}$
D. $\frac{1}{2}\pi.a^{2}\sqrt{3}$
Câu 9: Các khoảng đồng biến của hàm số $x^{4}-8x^{2}-4$ là :
A. $(-\infty ;-2)$ và $(2;+\infty )$
B. $(-2;0)$ và $(2;+\infty )$
C. $(-\infty ;-2)$ và $(0;2)$
D. $(-2;0)$ và $(0;2)$
Câu 10: Cho hàm số $y=\frac{2x-1}{x-2}$. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng $(\frac{1}{2};+\infty )$
B. Hàm số nghịch biến trên $(2;+\infty )$
C. Hàm số đồng biến trên khoảng $(2;+\infty )$
D. Hàm số đồng biến trên khoảng $(\frac{1}{2};+\infty )$
Câu 11: Hàm số nào sau đây đồng biến trên $(-\infty;+\infty )$
A. $y=x^{3}-3x$
B. $y=\frac{x-1}{x+2}$
C. $y=\frac{x+1}{x+3}$
D. $y=x^{3}+2x$
Câu 12: Cho tứ diện đều ABCD, khi quay tứ diện đó xung quanh trục là AB có bao nhiêu hình nón khác nhau được tạo thành?
A. 1
B. 3
C. 2
D. 0
Câu 13: Cho bốn điểm A, B, C, D cùng thuộc một mặt cầu và $\widehat{ADB}=\widehat{BDC}=\widehat{CDA}=90^{\circ}$. Một đường kính của mặt cầu đó là:
A. AB
B. BC
C. AC
D. DE (với $\vec{DE}=3\vec{DG}$, G là trọng tâm tam giác ABC)
Câu 14: Tìm các mệnh đề đúng trong các mệnh đề sau:
A. Hàm số $y=(\frac{\sqrt{3}}{2})^{x}$ đồng biến trên khoảng $(-\infty ;+\infty)$
B. Hàm số $y=(\sqrt{5}^{x}$ nghịch biến trên khoảng $(-\infty ;+\infty)$
C. Đồ thị các hàm số $y=4^{x}$ và $\log _{4}x$ đối xứng nhau qua đường phân giác y = x
D. Hàm số $y=\pi ^{x}$ luôn đi qua điểm (1;0)
Câu 15: Tìm tất cả các giá trị thực của m đề hàm số $y=x^{3}+x^{2}+mx+1$ đồng biến trên R.
A. $m\leq \frac{1}{3}$
B. $m\leq \frac{4}{3}$
C. $m\geq \frac{1}{3}$
D. $m\geq \frac{4}{3}$
Câu 16: Tính đạo hàm của $y=10^{x}$.
A. $y^{'}=x10^{x-1}$
B. $y^{'}=10^{x}ln10$.
C. $y^{'}=10^{x}$.
D. $y^{'}=\frac{10^{x}}{ln10}$
Câu 17: Một người gửi tiết kiệm với lãi suất 7,2%/năm và lãi hàng năm được nhập vào vốn. Hỏi sau bao nhiêu năm người đó thu được gấp đôi số tiền ban đầu?
A. 7
B. 8
C. 9
D. 10
Câu 18: Cho hình nón tròn xoay có chiều cao h =20(cm), bán kính đáy r=25(cm). Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là 12(cm). Tính diện tích của thiết diện đó.
A. S = 500$cm^{2}$
B. S = 400$cm^{2}$
C. S = 300$cm^{2}$
D. S = 406$cm^{2}$
Câu 19: Cho x, y là các số thực lớn hơn 1 thoả mãn $x^{2}-6y^{2}=xy$. Tính $M=\frac{1+log_{12}x+log_{12}x}{2log_{12}(x+3y)}.
A. $\frac{1}{4}$
B. 1
C. $\frac{1}{2}$
D. $\frac{1}{3}$
Câu 20: Cho hàm số $f(x)=\left ( x^{1+\frac{1}{2log_{4}x}}+8^{\frac{1}{3log_{x^{2}}2}}+1 \right )^{\frac{1}{2}}-1$ với 0 < x và x khác 1.Tính giá trị của biếu thức $P=f(f(2017))$.
A. P = 2016
B. P = 1009
C. P = 2017
D. P = 1008
Câu 21: Cho hàm số $f(x)=log_{2}(x^{2}+1)$. Hãy tính f^{'}(1).
A. $f^{'}(1)=\frac{1}{2}$
B. $f^{'}(1)=\frac{1}{2}ln2$
C. $f^{'}(1)=\frac{1}{ln2}$
D. $f^{'}(1)=2log_{2}2$
Câu 22: Kí hiệu $R_{1}, R_{2}, R_{3}$ là bán kính của các mặt cầu ngoại tiếp, nội tiếp và tiếp xúc với cạnh đáy của một hình lập phương. Khi ấy:
A. $R_{1}>R_{2}> R_{3}$
B. $R_{2}>R_{3}, R_{1}$
C.$R_{1}>R_{3}> R_{2}$
D.$R_{3}>R_{1}> R_{2}$$
Câu 23: Cho tam giác đều ABC cạnh a. Gọi (P) là mặt phẳng đi qua BC và vuông góc với mp(ABC). Trong mặt phẳng (P), xét đường tròn (C) đường kính BC. Bán kính mặt cầu (S) đi qua (C) và điểm A là:
A. $a\sqrt{3}$
B. $\frac{a\sqrt{3}}{2}$
C. $\frac{a\sqrt{3}}{3}$
D. $\frac{a\sqrt{3}}{4}$
Câu 24: Cho a, b là các số thực dương khác 1 và thoả mãn a.b khác 1. Rút gọn biểu thức $P=(log_{a}b+log_{b}a+2)(log_{a}b-log_{ab}b)log_{b}a-1$.
A. $P=log_{b}a$
B. 1
C. 0
D. $P=log_{a}b$
Câu 25: Cho a, b, c là các số thực dương thoả mãn $a^{2}=bc$. Tính P = 2.lna - lnb - lnc
A. $2ln(\frac{a}{b.c})$
B. 1
C. $2ln(\frac{a}{b.c})$
D. 0
Câu 26: Cho hình lăng trụ tam giác đều có các cạnh đều bằng a. Diện tích mặt cầu ngoại tiếp hình lăng trụ là:
A. $7\pi a^{2}$
B. $\frac{7\pi a^{2}}{2}$
D. $\frac{7\pi a^{2}}{3}$
C. $\frac{7\pi a^{2}}{6}$
Câu 27: Cho a, b, c là các số thực dương khác 1 thoả mãn $log_{a}b^{2}=x, log_{b^{2}}\sqrt{c}=y$. Tính giá trị của biểu thức P= $log_{c}a
A. $\frac{2}{xy}$
B. $2.xy$
C. $\frac{1}{2xy}$
D. $\frac{xy}{2}$
Câu 28: Đạo hàm của hàm số y=\sqrt[5]{ln^{3}5x} là:
A. $y^{'}=\frac{3}{x\sqrt[5]{ln^{3}5x}}$
B. $y^{'}=\frac{3}{x\sqrt[5]{ln^{2}5x}}$
C. $y^{'}=\frac{3}{5\sqrt[5]{ln^{2}5x}}$
D. $y^{'}=\frac{3}{5x\sqrt[5]{ln^{2}5x}}$
Câu 29: Cho tứ diện ABCD có DA vuông góc với mặt phẳng (ABC), Kí hiệu $V_{1}$, $V_{2}$, $V_{3}$ lần lượt là thể tích của hình tròn xoay sinh bởi tam giác ABD khi quay xung quanh AD, tam giác ABC khi quay quanh AB, tam giác BDC quay quanh BC. Mệnh đề nào sau đây đúng?
A. $V_{1}+V_{2}=V_{3}$
B. $V_{1}+V_{3}=V_{2}$
C. $V_{2}+V_{3}=V_{1}$
D. $V_{1}=V_{2}=V_{3}$
Câu 30: Cho p, q là các số thực dương khác 1 thoả mãn $log_{9}p=log_{12}q=log_{16}(p+q)$. Tính giá trị của $\frac{p}{q}$.
A. $\frac{1-\sqrt{5}}{2}$
B. $\frac{-1-\sqrt{5}}{2}$
C. $\frac{-1+\sqrt{5}}{2}$
D. $\frac{1+\sqrt{5}}{2}$
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận