Dạng bài tập Tính vận tốc, tốc độ, độ dịch chuyển trong chuyển động thẳng
PHẦN CHƯƠNG II: MÔ TẢ CHUYỂN ĐỘNG
Dạng 1: Tính vận tốc, tốc độ, độ dịch chuyển trong chuyển động thẳng
Bài tập 1: Một ô tô chạy từ địa điểm A đến địa điểm B với vận tốc 40 km/h. Sau đó ô tô quay trở về A với tốc độ 60 km/h. Giả sử ô tô luôn chuyển động thẳng đều.
a) Tính tốc độ trung bình của ô tô trên cả đoạn đường đi và về.
b) Tính vận tốc trung bình của ô tô trên cả đoạn đường đi và về.
Bài tập 2: Một người bắt đầu cho xe máy chạy trên một đoạn đường thẳng: trong 10 giây đầu xe chạy được quãng đường 50 m, trong 10 giây tiếp theo xe chạy được 100 m. Tốc độ trung bình của xe máy trong 20 giây đầu tiên là bao nhiêu?
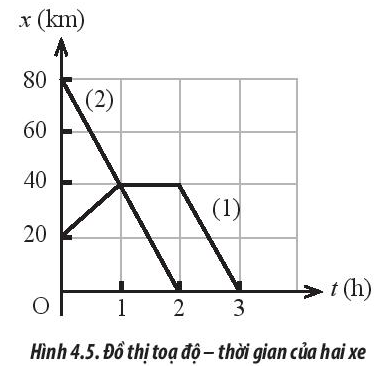
Bài tập 3: Hình 4.5 mô tả đồ thị tọa độ - thời gian của hai xe, hãy nêu đặc điểm chuyển động của mỗi xe.
Bài tập 1:
a) Tốc độ trung bình trên cả đoạn đường đi và về:
$v_{tb}=\frac{2AB}{t_{1}+t_{2}}=\frac{2AB}{\frac{AB}{v_{1}}+\frac{AB}{v_{2}}}=\frac{2v_{1}.v_{2}}{v_{1}+v_{2}}=\frac{2.40.60}{40+60}=48 km/h$
b) Vận tốc trung bình trên cả đoạn đường đi và về:
$v_{tb}=\frac{d}{t_{1}+t_{2}}=\frac{0}{t_{1}+t_{2}}=0 km/h$
Bài tập 2:
Tốc độ trung bình của xe máy trong 20 giây đầu tiên:
$v_{tb}=\frac{s_{1}+s_{2}}{t_{1}+t_{2}}=\frac{150}{20}=7,5 m/s$
Bài tập 3:
Chuyển động của xe 1:
- Trong khoảng thời gian từ 0 đến 1 h, xe chuyển động đều theo chiều dương với tốc độ $v=\frac{s}{\Delta t}=\frac{40-0}{1-0}$ = 20 km/h
- Trong khoảng thời gian từ 1 h đến 2 h, xe đứng yên.
- Trong khoảng thời gian từ 2 h đến 3 h, xe chuyển động đều theo chiều âm với tốc độ $v=\frac{s}{\Delta t}=\frac{40-0}{3-2}$ = 40 km/h
Chuyển động của xe 2: Trong khoảng thời gian từ 0 đến 2 h, xe chuyển động đều theo chiều âm với tốc độ $v=\frac{s}{\Delta t}=\frac{80-0}{2-0}$= 40 km/h

Bình luận