Dạng bài tập Tính các loại sai số và viết kết quả phép đo
PHẦN CHƯƠNG I: MỞ ĐẦU
Dạng: Tính các loại sai số và viết kết quả phép đo
Bài tập 1: Một vật có khối lượng m và thể tích V, có khối lượng riêng $\rho$ được xác định bằng công thức $\rho=\frac{m}{V}$. Biết sai số tương đối của m và V lần lượt là 12% và 5%. Hãy xác định sai số tương đối của $\rho$.
Bài tập 2: Một bánh xe có bán kính là R = 10,0 ± 0,5 cm. Sai số tương đối của chu vi bánh xe là bao nhiêu?
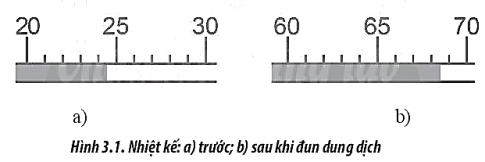
Bài tập 3: Hình 3.1 thể hiện nhiệt kế đo nhiệt độ t1 ($^{\circ}C$) và t2 ($^{\circ}C$) của một dung dịch trước và sau khi đun. Hãy xác định và ghi kết quả độ tăng nhiệt độ t của dung dịch này.
Bài tập 1:
Vì $\rho=\frac{m}{V}$
Nên ta có: $\delta\rho=\delta m+\delta V$=12%+5%=17%
Bài tập 2:
Sai số tương đối của bán kính: $\delta R=\frac{\Delta R}{\overline{R}}=\frac{0,5}{10,0}=5$%
Chu vi hình tròn: $p=2.\pi.R$
=> $\delta p=\delta R=5$%
Bài tập 3:
Độ chia nhỏ nhất của dụng cụ đo là $1^{\circ}$ nên sai số hệ thống là $0,5^{\circ}$.
Từ hình vẽ, ta đọc được $t_{1}=24,0\pm0,5^{\circ}C$ và $t_{2}=68,0\pm0,5^{\circ}C$
Suy ra: $\overline{t}=\overline{t_{1}}-\overline{t_{2}}=68,0-24,0=40,0^{\circ}C$
Sai số tuyệt đối: $\Delta t=\Delta t_{2}+\Delta t_{1}=0,5+0,5=1,0^{\circ}C$
Vậy độ tăng nhiệt độ của dung dịch là: $t=\overline{t}+\Delta t=44,0\pm 1,0^{\circ}C$
Giải những bài tập khác
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận