A. KIẾN THỨC TRỌNG TÂM

Chủ đề: Mệnh đề. Tập hợp

- Mệnh đề là một khẳng định đúng hoặc sai (không thể vừa đúng vừa sai)

- Mệnh đề phủ định $\bar{P}$: Nếu P đúng thì $\bar{P}$ sai, nếu P sai thì $\bar{P}$ đúng

- Mệnh đề kéo theo: P $\Rightarrow $ Q. Mệnh đề kéo theo chỉ sai khi P đúng và Q sai. P là điều kiện đủ để có Q, Q là điều kiện cần để có P

- Mệnh đề đảo: Q $\Rightarrow $ P

- Nếu  P $\Rightarrow $ Q và Q $\Rightarrow $ P đều đúng thì P và Q là hai mệnh đề tương đương ($P\Leftrightarrow Q $)

- Mệnh đề "$\forall x\in M,P(x)$" đúng nếu với mọi $x_{0}\in M,P(x_{0})$ đúng

Mệnh đề "$\exists x\in M,P(x)$" đúng nếu có $x_{0}\in M$ sao cho $P(x_{0})$ đúng

- $\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}$

- A = B nếu $A\subset B$ và $B\subset A$

- Một số tập con của tập số thực: 

- Hợp hai tập hợp: $A\cup B=$ {x | x $\in $ A hoặc x $\in $ B}

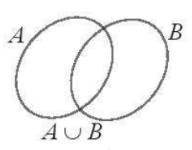
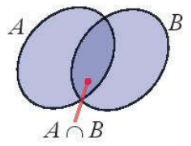
- Giao hai tập hợp: $A\cap  B=$ {x | x $\in $ A và x $\in $ B}

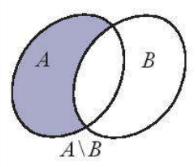
- Hiệu hai tập hợp: A \ B = {x | x $\in $ A và x $\notin $ B}

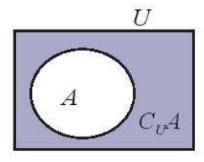
- Phần bù của tập con: $C_{U}A$

Chủ đề: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

- Bất phương trình bậc nhất hai ẩn x, y: ax + by + c < 0; ax + by + c > 0; ax + by + c $\leq $ 0; ax + by  + c $\geq $ 0 (a, b không đồng thời bằng 0)

- Biểu diễn miền nghiệm bất phương trình: 

+ Trên mặt phẳng Oxy, vẽ $\Delta $: ax + by + c = 0

+ Lấy $(x_{0};y_{0})$ không thuộc $\Delta $. Tính $ax_{0}+by_{0}+c$

+ Nếu $ax_{0}+by_{0}+c$ < 0 thì miền nghiệm là nửa mặt phẳng (không kể $\Delta $) chứa $(x_{0};y_{0})$

Nếu $ax_{0}+by_{0}+c$ > 0 thì miền nghiệm là nửa mặt phẳng (không kể $\Delta $) không chứa $(x_{0};y_{0})$

- Biểu diễn miền nghiệm hệ bất phương trình: 

+ Biểu diễn miền nghiệm của mỗi bất phương trình trong hệ trên cùng mặt phẳng tọa độ

+ Giao các miền nghiệm là miền nghiệm của hệ bất phương trình

Chủ đề: Hàm số bậc hai và đồ thị

- Hàm số y = f(x) xác định trên khoảng (a;b):

+ Hàm số đồng biến trên (a;b) nếu $\forall x_{1},x_{2}\in (a;b),x_{1}<x_{2}\Rightarrow f(x_{1})<f(x_{2})$

+ Hàm số nghịch biến trên (a;b) nếu $\forall x_{1},x_{2}\in (a;b),x_{1}<x_{2}\Rightarrow f(x_{1})>f(x_{2})$

- Hàm số bậc hai: y = f(x) = $ax^{2}+bx+c$ ($a\neq 0$). Tập xác định $\mathbb{R}$

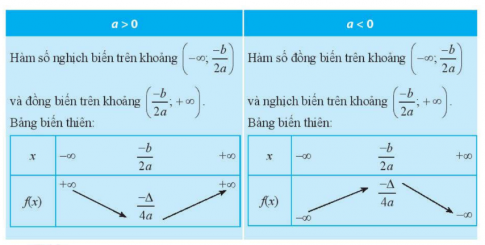
- Đồ thị hàm số bậc hai là một parabol đỉnh S($-\frac{b}{2a};-\frac{\Delta }{4a}$), trục đối xứng x = $-\frac{b}{2a}$:

+ Bề lõm quay lên nếu a > 0, quay xuống nếu a < 0

+ Đồ thị đi qua điểm có tọa độ (0;c)

- Sự biến thiên của hàm số bậc hai:

Chủ đề: Hệ thức lượng trong tam giác

- Giá trị lượng giác của hai góc bù nhau:

$\sin (90^{\circ}-\alpha )=\cos \alpha $

$\cos (90^{\circ}-\alpha )=\sin \alpha $

$\tan (90^{\circ}-\alpha )=\cot \alpha $

$\cot (90^{\circ}-\alpha )=\tan \alpha $

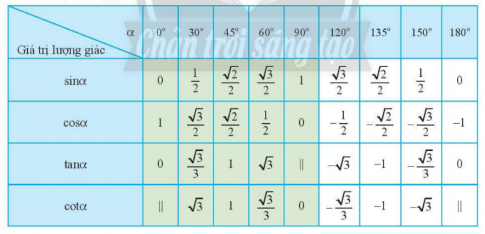
- Với mọi $\alpha $ thỏa mãn $0^{\circ}\leq \alpha \leq 180^{\circ}$:

$\sin (180^{\circ}-\alpha )=\sin \alpha$ 

$\cos (180^{\circ}-\alpha )=-\cos \alpha $

$\tan (180^{\circ}-\alpha )=-\tan \alpha (\alpha \neq 90^{\circ})$

$\cot (180^{\circ}-\alpha )=-\cot \alpha (0^{\circ}<\alpha <180^{\circ})$

- Bảng giá trị lượng giác một số góc đặc biệt:

- Định lí Côsin: Tam giác ABC có BC = a, CA = b, AB = c

$a^{2}=b^{2}+c^{2}-2bc\cos A$

$b^{2}=c^{2}+a^{2}-2ca\cos B$

$c^{2}=a^{2}+b^{2}-2ab\cos C$

- Định lí Sin: Tam giác ABC có BC = a, CA = b, AB = c, R - bán kính đường tròn ngoại tiếp: $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$

- Công thức tính diện tích tam giác:

$S=\frac{1}{2}ah_{a}=\frac{1}{2}bh_{b}=\frac{1}{2}ch_{c}$

$S=\frac{1}{2}ab\sin C=\frac{1}{2}bc\sin A=\frac{1}{2}ac\sin B$

$S=\frac{abc}{4R}$

$S=pr$

$S=\sqrt{p(p-a)(p-b)(p-c)}$ (công thức Heron)

Chủ đề: Vectơ

- Hai vectơ cùng phương nếu giá song song hoặc trùng nhau

- $\vec{a}=\vec{b}$ nếu cùng hướng và cùng độ dài

- Tổng hai vectơ: 

+ Quy tắc ba điểm: $\vec{MN}+\vec{NP}=\vec{MP}$

+ Quy tắc hình bình hành: Nếu OABC là hình bình hành thì $\vec{OA}+\vec{OC}=\vec{OB}$

- Tính chất phép cộng vectơ:

+ Giao hoán: $\vec{a}+\vec{b}=\vec{b}+\vec{a}$

+ Kết hợp: $(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$

+ $\vec{a}+\vec{0}=\vec{0}+\vec{a}=\vec{a}$

- Hiệu hai vectơ: $\vec{a}-\vec{b}=\vec{a}+(-\vec{b})$

- M là trung điểm của AB khi và chỉ khi $\vec{MA}+\vec{MB}=\vec{0}$

- G là trọng tâm tam giác ABC khi và chỉ khi $\vec{GA}+\vec{GB}+\vec{GC}=\vec{0}$

- Tích của một số và một vectơ: k$\vec{a}$ ($k\neq 0$; $\vec{a}\neq \vec{0}$)

+ k$\vec{a}$ cùng hướng với $\vec{a}$ nếu k > 0

+ k$\vec{a}$ ngược hướng với $\vec{a}$ nếu k < 0

+ Độ dài: |k|.|$\vec{a}$|

- Tính chất: 

$k(\vec{a}+\vec{b})=k\vec{a}+k\vec{b}$

$(h+k)\vec{a}=h\vec{a}+k\vec{a}$

$h(k\vec{a})=(hk)\vec{a}$

$1.\vec{a}=\vec{a}$

$(-1).\vec{a}=-\vec{a}$

- $\vec{a}$ và $\vec{b}$ cùng phương khi và chỉ khi $\vec{a}=k\vec{b}$

- Tích vô hướng hai vectơ: $\vec{a}.\vec{b}=\left | \vec{a} \right |.\left | \vec{b} \right |.\cos (\vec{a};\vec{b})$

- Tính chất: 

$\vec{a}.\vec{b}=\vec{b}.\vec{a}$

$\vec{a}(\vec{b}+\vec{c})=\vec{a}.\vec{b}+\vec{a}.\vec{c}$

$(k\vec{a}).\vec{b}=k(\vec{a}.\vec{b})=\vec{a}.(k\vec{b})$

Chủ đề: Số gần đúng và sai số

- Số gần đúng: a; số đúng: $\bar{a}$; độ chính xác d; sai số tuyệt đối: $\Delta _{a}=\left | \bar{a}-a \right |$

- Sai số tương đối: $\delta _{a}=\frac{\Delta _{a}}{\left | a \right |}$

- Xác định số quy tròn:

+ Tìm hàng của chữ số khác 0 đầu tiên bên trái của d

+ Quy tròn số a ở hàng gấp 10 lần hàng tìm  được ở Bước 1

Chủ đề: Số trung bình. Trung vị. Mốt

- Số trung bình: $\bar{x}=\frac{x_{1}+x_{2}+...+x_{n}}{n}$

hoặc mẫu số liệu có dạng bảng tần số:

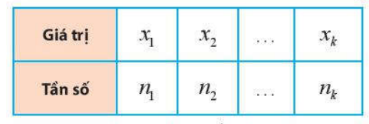
thì $\bar{x}=\frac{n_{1}x_{1}+n_{2}x_{2}+...+n_{k}x_{k}}{n}$

- Trung vị:

+ Nếu $n=2k+1,k\in \mathbb{N}$ thì $M_{e}=x_{k+1}$

+ Nếu $n=2k,k\in \mathbb{N}$ thì $M_{e}=\frac{1}{2}(x_{k}+x_{k+1})$

- Tứ phân vị: Tứ phân vị thứ nhất ($Q_{1}$), thứ hai ($Q_{2}$), thứ ba ($Q_{3}$) chia mẫu số liệu thành bốn phần đều nhau ($Q_{2}$: trung vị của mẫu; $Q_{1}$: trung vị của nửa số liệu bên trái $Q_{2}$; $Q_{3}$: trung vị của nửa số liệu bên phải $Q_{2}$

- Mốt ($M_{o}$): giá trị có tần số lớn nhất

- Khoảng biến thiên: $R=x_{n}-x_{1}$

- Khoảng tứ phân vị: $\Delta _{Q}=Q_{3}-Q_{1}$

- Phương sai: $S^{2}=\frac{1}{n}\left [ (x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+...+(x_{n}-\bar{x})^{2} \right ]$

- Độ lệch chuẩn: $S=\sqrt{S^{2}}$