Bài tập dạng vectơ
Dạng 5: Vectơ
Bài tập 1: Cho tam giác ABC có AM là trung tuyến. Gọi I là trung điểm của AM và K là một điểm trên cạnh AC sao cho AK = $\frac{1}{3}$AC. Chứng minh ba điểm B, I, K thẳng hàng.
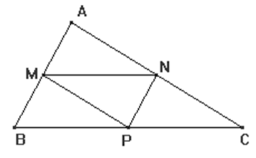
Bài tập 2: Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của AB, AC, BC.
a) Tìm $\vec{AM}-\vec{AN}$; $\vec{MN}-\vec{NC}$; $\vec{MN}-\vec{PN}$; $\vec{BP}-\vec{CP}$
b) Phân tích $\vec{AM}$ theo hai vectơ $\vec{MN}$; $\vec{MP}$
Bài tập 1:
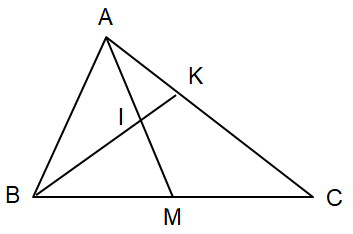
Ta có: $\vec{BK}=\vec{BA}+\vec{AK}=\vec{BA}+\frac{1}{3}\vec{AC}$
$=\vec{BA}+\frac{1}{3}(\vec{AB}+\vec{BC})=\vec{BA}+\frac{1}{3}\vec{AB}+\frac{1}{3}\vec{BC}$
$=\frac{2}{3}\vec{BA}+\frac{1}{3}\vec{BC}=\frac{1}{3}(2\vec{BA}+\vec{BC})$
$\vec{BI}=\vec{BA}+\vec{AI}=\frac{1}{4}(2\vec{BA}+\vec{BC})$
Suy ra: $\vec{BK}=\frac{4}{3}\vec{BI}$. Do đó: B, I, K thẳng hàng.
Bài tập 2:
a) $\vec{AM}-\vec{AN}=\vec{NM}$
$\vec{MN}-\vec{NC}=\vec{MN}-\vec{MP}=\vec{PN}$ (vì $\vec{NC}=\vec{MP}$)
$\vec{MN}-\vec{PN}=\vec{MN}+\vec{NP}=\vec{MP}$
$\vec{BP}-\vec{CP}=\vec{BP}+\vec{PC}=\vec{BC}$
b) $\vec{AM}=\vec{NP}=\vec{MP}-\vec{MN}$
Xem toàn bộ: Đề cương ôn tập Toán 10 chân trời sáng tạo học kì 1

Bình luận