Dạng bài tập Tính gia tốc, và các đại lượng khác trong chuyển động biến đổi đều
PHẦN CHƯƠNG III: CHUYỂN ĐỘNG BIẾN ĐỔI ĐỀU
Dạng 1: Tính gia tốc, và các đại lượng khác trong chuyển động biến đổi đều
Bài tập 1: Một xe chuyển động chậm dần đều với tốc độ đầu 36 km/h. Trong giây thứ 6 xe đi được 7,25 m. Tính quãng đường xe đi được trong giây thứ 8.
Bài tập 2: Tại hiện trường một vụ tai nạn trên đường quốc lộ ngoài đô thị, cảnh sát phát hiện vết trượt kéo dài 50 m. Qua các đo đạc trên mặt đường, cảnh sát kết luận gia tốc của ô tô trong quá trình giảm tốc có độ lớn 6,5 m/s$^{2}$. Nếu tốc độ giới hạn trên làn đường được quy định là 80 km/h thì ô tô này có vượt quá tốc độ cho phép không? Giả sử trong quá trình giảm tốc, ô tô chuyển động chậm dần đều.
Bài tập 3: Xét một người đi xe máy trên một đoạn đường thẳng. Tốc độ của xe máy tại mỗi thời điểm được ghi lại trong bảng dưới đây.
t (s) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
v (m/s) | 0 | 15 | 30 | 30 | 20 | 10 | 0 |
a) Vẽ đồ thị vận tốc thời gian của xe máy.
b) Nhận xét tính chất chuyển động của xe máy.
c) Xác định gia tốc của xe máy trong 10 s đầu tiên và trong 15 s cuối cùng.
d) Từ đồ thị vận tốc thời gian, tính quãng đường mà người này đã đi được sau 30 s kể từ lúc bắt đầu chuyển động.
Bài tập 1:
Đổi: vo = 36 km/h = 10 m/s.
Quãng đường xe đi được trong giây thứ 6 là:
$s_{6}=v_{o}.6+\frac{a.6^{2}}{2}-v_{o}.5-\frac{a.5^{2}}{2}=7,25m$
Suy ra a = - 0,5 m/s$^{2}$.
Quãng đường xe đi được trong giây thứ 8 là:
$s_{8}=v_{o}.8+\frac{a.8^{2}}{2}-v_{o}.7-\frac{a.7^{2}}{2}=6,25m$
Bài tập 2:
Tốc độ của ô tô là: $v=\sqrt{2as}=\sqrt{2.6,5.50}$(m/s)≈91,8km/h>80kmh
=> Trên làn đường này, ô tô đã vượt quá tốc độ cho phép
Bài tập 3:
a) Đồ thị vận tốc - thời gian của xe máy
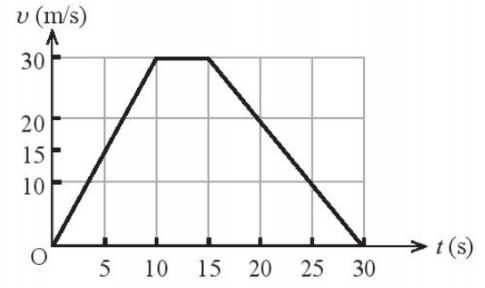
b) Trong khoảng thời gian từ 0 đến 10 s: xe chuyển động thẳng nhanh dần đều.
Trong khoảng thời gian từ 10 đến 15 s: xe chuyển động thẳng đều.
Trong khoảng thời gian từ 15 đến 30 s: xe chuyển động thẳng chậm dần đều.
c) Trong 10 s đầu tiên, gia tốc:
$a=\frac{\Delta v}{\Delta t}=\frac{30-0}{10-0}= 3 m/s^{2}$
Trong 15 s cuối cùng, gia tốc:
$a=\frac{\Delta v}{\Delta t}=\frac{0-30}{30-15}= -2 m/s^{2}$
d) Quãng đường đi được trong 30 s bằng diện tích giới hạn phía dưới đồ thị
$s=\frac{(5+30).30}{2}=525 m$
Giải những bài tập khác
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận