Dạng bài tập Tính tổng hợp lực - Phân tích lực
PHẦN CHƯƠNG V: MOMENT LỰC. ĐIỀU KIỆN CÂN BẦNG
Dạng 1: Tính tổng hợp lực - Phân tích lực
Bài tập 1: Hai lực $\vec{F}_{1}, \vec{F}_{2}$ song song, cùng chiều, cách nhau một đoạn 20 cm. Độ lớn của lực $\vec{F}_{1}$ là 18 N và của lực tổng hợp $\vec{F}$ là 24 N. Hỏi độ lớn của lực $\vec{F}_{2}$ và điểm đặt của lực tổng hợp cách điểm đặt của lực $\vec{F}_{2}$ một đoạn là bao nhiêu?
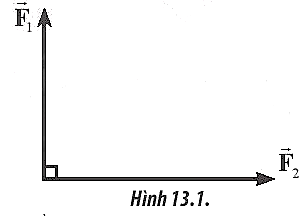
Bài tập 2: Hai lực có giá đồng quy, vuông góc có độ lớn các lực thành phần là F1 = 6N và F2 = 8N (Hình 13.1). Xác định độ lớn của lực tổng hợp và góc hợp giữa vectơ lực tổng hợp và vectơ lực $\vec{F}_{1}$
Bài tập 3: Đặt tại hai đầu thanh AB dài 60 cm hai lực song song cùng chiều và vuông góc với AB. Lực tổng hợp $\vec{F}$ được xác định đặt tại O cách A một khoảng 15 cm và có độ lớn 12 N (Hình 13.2). Độ lớn của lực $\vec{F}_{1}$ bằng bao nhiêu?
Bài tập 1:
F2 = F - F1 = 6N
$\left\{\begin{matrix}\frac{d_{2}}{d_{1}}=\frac{3}{1}\\ d_{2}+d_{1}=20 cm \end{matrix}\right.\Rightarrow \left\{\begin{matrix}d_{1}=5cm\\ d_{2}=15cm\end{matrix}\right.$
Bài tập 2:
Độ lớn hợp lực: $F=\sqrt{F_{1}^{2}+F_{2}^{2}}$= 10 N.
$tan\alpha=\frac{F_{1}}{F_{2}}=\frac{8}{6} \Rightarrow \alpha \approx 53,3^{\circ}$
Bài tập 3:
Ta có: $\frac{F_{1}}{F_{2}}=\frac{d_{2}}{d_{1}}\Rightarrow\frac{F_{1}}{F_{2}}=\frac{45}{15} \Rightarrow F_{1}-3F_{2}=0$
Lực tổng hợp $\vec{F}$ có độ lớn 12 N ⇒F1+F2=12
Ta tìm được F1=9 N.
Giải những bài tập khác
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận