Giải hoạt động thực hành 3 trang 73 toán 12 tập 1 ctst
Giải hoạt động thực hành 3 trang 73 toán 12 tập 1 ctst
a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm ở Ví dụ 4 sau khi đã loại bỏ các giá trị ngoại lệ. Em có nhận xét gì về khoảng biến thiên, khoảng tứ phân vị vừa tìm được và khoảng biến thiên, khoảng tứ phân vị ban đầu?
Hằng ngày ông Thắng đều đi xe buýt từ nhà đến cơ quan. Dưới đây là bảng thống kê thời gian của 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan.

b) Hãy so sánh độ phân tán của nửa giữa hai mẫu số liệu chiều cao của các học sinh nữ lớp 12C và 12D ở hoạt động Thực hành 1.

a) Cỡ mẫu n = 100.
Gọi ![]() là mẫu số liệu gốc gồm thời gian 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan và được xếp theo thứ tự không giảm.
là mẫu số liệu gốc gồm thời gian 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan và được xếp theo thứ tự không giảm.
Khoảng biến thiên ![]() (phút)
(phút)
Ta có ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Tứ phân vị thứ nhất của mẫu số liệu gốc là ![]() . Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
. Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
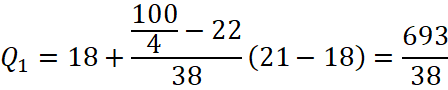
Tứ phân vị thứ ba của mẫu số liệu gốc là ![]() . Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
. Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
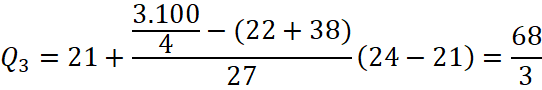
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
![]()
Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu ![]() hoặc
hoặc
![]()
Hay ![]() hoặc
hoặc ![]()
Vậy các giá trị ngoại lệ thuộc khoảng ![]() ;
; ![]() ;
; ![]() ;
; ![]()
Khoảng biến thiên của mẫu số liệu ghép nhóm sau khi loại bỏ giá trị ngoại lệ là:
![]() (phút)
(phút)
Gọi ![]() là mẫu số liệu gốc gồm thời gian 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan sau khi đã loại bỏ các giá trị ngoại lệ và được xếp theo thứ tự không giảm.
là mẫu số liệu gốc gồm thời gian 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan sau khi đã loại bỏ các giá trị ngoại lệ và được xếp theo thứ tự không giảm.
Ta có: Ta có ![]() ;
; ![]() .
.
Tứ phân vị thứ nhất của mẫu số liệu gốc là ![]() . Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
. Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
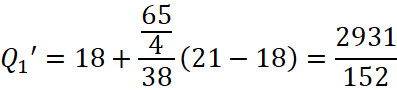
Tứ phân vị thứ ba của mẫu số liệu gốc là ![]() . Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
. Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
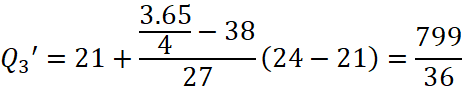
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
![]()
Nhận xét: Như vậy, sau khi loại bỏ giá trị ngoại lệ, khoảng biến thiên mới giảm mạnh còn khoảng tứ phân vị thì không bị ảnh hưởng nhiều.
b) Cỡ mẫu: n = 25.
Gọi ![]() là mẫu số liệu của chiều cao các bạn học sinh nữ lớp 12C được xếp theo thứ tự không giảm.
là mẫu số liệu của chiều cao các bạn học sinh nữ lớp 12C được xếp theo thứ tự không giảm.
Ta có ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Tứ phân vị thứ nhất của mẫu số liệu gốc là ![]() . Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
. Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
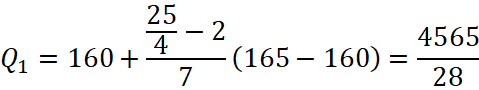
Tứ phân vị thứ ba của mẫu số liệu gốc là ![]() . Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
. Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
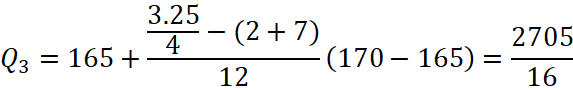
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
![]()
Gọi ![]() là mẫu số liệu gốc của chiều cao của các bạn học sinh nữ lớp 12D được xếp theo thứ tự không giảm.
là mẫu số liệu gốc của chiều cao của các bạn học sinh nữ lớp 12D được xếp theo thứ tự không giảm.
Ta có ![]() ;
; ![]() ;
; ![]() ;
; ![]() ; và
; và ![]() .
.
Tứ phân vị thứ nhất của mẫu số liệu gốc là ![]() . Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
. Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
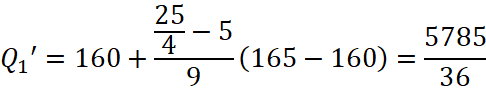
Tứ phân vị thứ ba của mẫu số liệu gốc là ![]() . Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
. Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
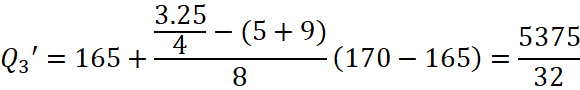
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
![]()
Ta có ![]() nên có thể kết luận chiều cao của các bạn học sinh nữ lớp 12D có độ phân tán lớn hơn lớp 12C.
nên có thể kết luận chiều cao của các bạn học sinh nữ lớp 12D có độ phân tán lớn hơn lớp 12C.
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận