1. ĐƯỜNG TRUNG TRỰC CỦA MỘT ĐOẠN THẲNG 

HĐKP1:

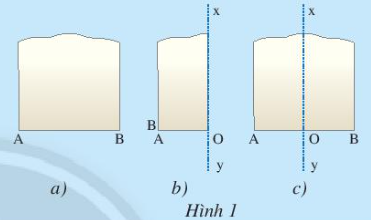
xy ⊥ AB tại trung điểm O.

⇒ Kết luận:

Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng ấy.

Ví dụ 1: SGK-tr67

Thực hành 1: 

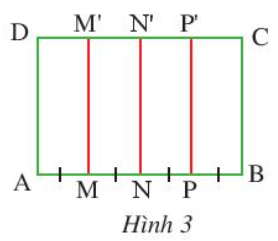
Có BC ⊥ AB

           MM' // BC  

=> MM' ⊥ AB hay MM' ⊥ AN

Tương tự ta có: NN' ⊥ AB, PP' ⊥ NB

AM = MN => M là trung điểm của AN. Mà M'M ⊥ AN

=> MM' là đường trung trực của AN

NP = PB => P là trung điểm của NB. Mà PP' ⊥ NB

=> PP' là đường trung trực của NB

 AM = MN = NP= PB => AN= NB => N là trung điểm của AB

NN' ⊥ AB. N là trung điểm của AB => NN' là đường trung trực của AB.

Vận dụng 1:

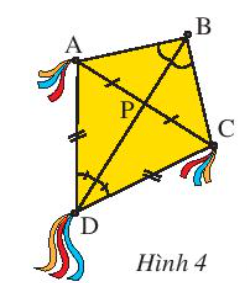
Xét ∆APD và ∆CPD có:

AD = CD

DP chung

$\widehat{ADP}=\widehat{CDP}$

=>  ∆APD = ∆CPD (g.c.g)

=> $\widehat{APD}=\widehat{CPD}$

mà $\widehat{APD}+\widehat{CPD}$ = 180°

=> 2$\widehat{APD}$ = 180°

=> $\widehat{APD}$ = 90°

=> DP ⊥ AP hay DP ⊥ AC

Mà P là trung điểm của AC

=> DP là đường trung trực của AC, hay DB là đường trung trực của AC.

2. TÍNH CHẤT CỦA ĐƯỜNG TRUNG TRỰC 

HĐKP2:

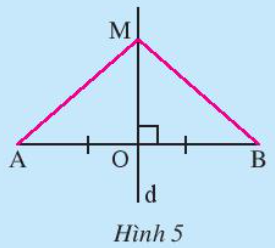
d là đường trung trực của AB tại điểm O 

=> ∆MOA và ∆MOB là hai tam giác vuông tại O.

Xét ∆MOA và ∆MOB cùng vuông tại đỉnh O ta có:

MO chung

AO = OB ( O là trung điểm của AB)

=> ∆MOA = ∆MOB (hai cạnh góc vuông)

=> MA = MB.

=> Kết luận:

Định lí 1:

Điểm nằm trên trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

Định lí 2:

Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Thực hành 2:

M thuộc đường thẳng d mà d là đường trung trực của AB

=> MA = MB

=> x + 2 = 7 

=> x = 7 - 2 = 5.

Vậy x = 5.

Vận dụng 2:

Ta có M thuộc 2 đường tròn tâm A và B

Mà bán kính đường tròn tâm A bằng với bán kính đường tròn tâm B

=> MA = MB

=> M cách đều hai đầu mút của đoạn thẳng B

=> M thuộc đường trung trực của AB

Tương tự ta có NA = NB

=> N cách đều hai đầu mút của đoạn thẳng AB

=> N thuộc đường trung trực của AB

=> MN là đường trung trực của AB.

Chú ý:

- Khi vẽ hai cung tròn trên, ta phải lấy bán kính lớn hơn $\frac{1}{2}$ AB thì hai cung tròn đó mới có hai điểm chung.

- Giao điểm của đường thẳng MN với đoạn thẳng AB là trung điểm của đoạn thẳng AB nên cách vẽ trên cũng là cách dựng trung điểm của đoạn thẳng bằng thước và compa.