CHƯƠNG IV. QUAN HỆ SONG SONG TRONG KHÔNG GIAN

BÀI 12: ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG

1. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG 

Hoạt động 1:

Từ hình vẽ ta thấy:

- Xà ngang nằm phía trên và không có điểm chung với mặt đất;

- Cột dọc thẳng đứng và có 1 điểm chung với mặt đất;

- Thanh chống nằm xiên và có 1 điểm chung với mặt đất;

- Thanh bên nằm hoàn toàn trên mặt đất, có vô số điểm chung với mặt đất.

Kết luận:

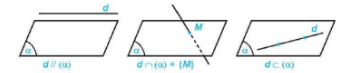
Cho đường thẳng d và mặt phẳng (α). Nếu d và (α) không có điểm chung thì ta nói d song song với (α) hay (α) song song với d và kí hiệu là d // (α) hay (α) //d.

Ngoài ra:

- Nếu d và (α) có một điểm chung duy nhất M thì ta nói d và (α) cắt nhau tại điểm M và kí hiệu d∩(α)={M} hay 

d∩=M.

- Nếu d và (α) có nhiều hơn một điểm chung thì ta nói d nằm trong (α) hay (α) chứa d và kí hiệu d⊂(α) hay (α)⊃d.

Câu hỏi:

Quan sát hình ảnh đã cho ta thấy:

- Đường thẳng được tạo bởi thanh ngang của cây cầu song song với mặt nước lúc tĩnh lặng.

Ví dụ 1: (SGK – tr.85).

Hướng dẫn giải (SGK – tr. 85).

Luyện tập 1:

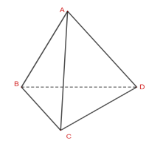
- Đường thẳng AC cắt các mặt phẳng: (BCD) và (ABD).

- Đường thẳng AC nằm trong mặt phẳng: (ABC) và (ACD).

2. ĐIỀU KIỆN VÀ TÍNH CHẤT CỦA ĐƯỜNG THẲNG 

Hoạt động 2:

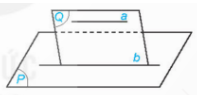
- Vì a thuộc Q nên nếu a cắt (P) tại M, thì M thuộc giao tuyến của (P) và (Q).

Vậy suy ra M thuộc b.

- Kết luận: Nếu a không nằm trong (P) và song song với b thuộc (P) thì a song song với (P) hay a và (P) không có điểm chung.

Kết luận:

Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P).

Câu hỏi:

Phát biểu trên không còn đúng nếu bỏ điều kiện "a không nằm trong mặt phẳng (P)". Vì khi đó, có thể a thuộc mặt phẳng (P).

Ví dụ 2:

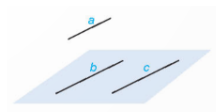
Ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng nên đường thẳng a không nằm trong mp(b, c). Vì đường thẳng a song song với đường thẳng b và đường thẳng b nằm trong mp(b, c) nên đường thẳng a song song với mp(b, c).

Luyện tập 2

+) Ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng nên: c không thuộc mp(a, b) 

Vì c//b và bmp(a, b) => c//mpa, b.

+) Ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng nên: b không thuộc mp(a, c)

Vì b//a và amp(a, c) => b//mp(a, c).

3. ĐIỂU KIỆN VÀ TÍNH CHẤT CỦA ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG ( TIẾP TỤC)

Ví dụ 3: (SKG – tr.86) 

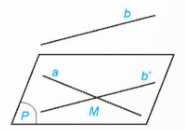
Chú ý:

Cho trước hai đường thẳng chéo nhau, có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.

Luyện tập 3

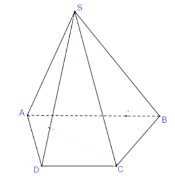
+) Nếu hai đường thẳng SD và AB không chéo nhau thì SD và AB đồng phẳng hay bốn điểm S, A, B, D đồng phẳng, trái với giả thiết S.ABCD là hình chóp. 

Do đó, hai đường thẳng SD và AB chéo nhau.

+) Ta có đường thẳng AB không nằm trong mặt phẳng (SCD) và AB // CD (giả thiết), 

CD⊂(SCD), 

Nên AB ∕∕ SCD.

Mà mặt phẳng (SCD) chứa đường thẳng SD. Vậy mặt phẳng (SCD) chứa đường thẳng SD và song song với AB.

Vận dụng

Dây nhợ được căng theo hàng gạch đầu tiên, các hàng gạch được xây thẳng hàng và mỗi viên gạch đều có cách cạnh đối diện song song với nhau, do đó mép trên của hàng gạch đầu là một đường thẳng song song với mặt đất nên dây nhợ khi căng song song với mặt đất. Tác dụng của việc căng dây nhợ để xây tường có độ thẳng, đứng và bằng.

Hoạt động 3:

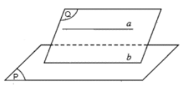
a) Hai đường thẳng a và b đều nằm trong mặt phẳng (Q) nên hai đường thẳng này không thể chéo nhau.

b) Giả sử hai đường thẳng a và b cắt nhau tại điểm I. Khi đó I$\in $ (P) vì I$\in $ b và b$\subset $ (P). Mặt khác I $\in $ a nên a cắt (P) tại I (vô lý do a song song với (P)). Vậy a // b hay hai đường thẳng a và b không thể cắt nhau.

Kết luận:

Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b song song với a.

Ví dụ 4: (SGK – Tr.86)

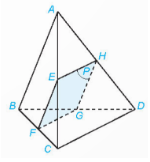
Luyện tập 4:

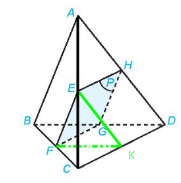
AB$\subset $ mp(ABC) ; AB//(Q) => mp(ABC)∩mp(Q) theo giao tuyến song song với AB.

Vẽ EF//AB (F$\in $BC) => mp(ABC)$\cap $mp(Q)=EF.

AD$\subset $mp(ACD);AD$\subset $mp(ABD);AD//mp(Q) 

=> {mp(Q)∩mp(ACD)  mp(Q)∩mp(ABD) theo giao tuyến song song với AD.

Vẽ EH//AD, (KCD) => mp(Q)$\cap $mp(ACD)=EK; pQmpABD=FK

Phần bài tập

Bài tập 4.16

a) Mệnh đề a) là mệnh đề đúng vì nếu a và (P) có điểm chung thì a cắt (P) hoặc a nằm trong (P) nên a không song song với (P).

b) Mệnh đề b) là mệnh đề sai vì nếu a và (P) có điểm chung thì a và (P) cắt nhau hoặc a nằm trong (P).

c) Mệnh đề c) là mệnh đề sai vì a có thể nằm trong (P).

d) Mệnh đề d) là mệnh đề sai vì a và b có thể cắt nhau.

Bài tập 4.20

Bài 4.20.

Cánh cửa có dạng hình chữ nhật nên mép trên cửa song song với mép dưới cửa. Mà mép dưới của cửa luôn tạo với mặt sàn một đường thẳng, do đó mép trên của cửa luôn song song với mặt sàn nhà.