1. HÀM SỐ CHẴN, HÀM SỐ LE, HÀM SỐ TUẦN HOÀN

1. Hàm số chẵn, hàm số lẻ.

HĐ1

a) Hàm số f(x) = x$^{2}$

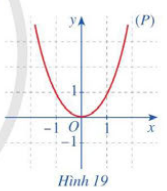
• Với x ∈ R, ta có: f(-x) = (-x)$^{2}$ = x$^{2}$

Do đó f(-x) = f(x)

• Trục đối xứng của (P) là đường thẳng x = 0, hay chính là trục Oy.

b) Hàm số g(x) = x

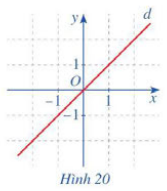
• Với x ∈ R, ta có: g-x=-x và -gx=-x.

Do đó g(-x) = -g(x).

• Gốc tọa độ O là tâm đối xứng của đường thẳng d.

=> Ta nói hàm số f(x) = x$^{2}$ là hàm số chẵn; hàm số g(x) = x là hàm số lẻ.

Khái niệm: Cho hàm số y = f(x) với tập xác định D.

• Hàm số y = f(x) được gọi là hàm số chẵn nếu ∀x ∈ D thì -x ∈ D và f(-x) = f(x).
• Hàm số y = f(x) được gọi là hàm số lẻ nếu ∀x ∈ D thì -x ∈ D và f(-x) = -f(x).

Chú ý

• Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.
• Đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.

Ví dụ 1: (SGK – tr.22).

Hướng dẫn giải (SGK – tr.22).

Luyện tập 1

a) Hàm số $g(x)= x^{3}$ là hàm số lẻ vì:

Tập xác định là $D=\mathbb{R}$;

$\forall x\in \mathbb{R}$ thì $-x\in \mathbb{R}$ và $g(-x)=(-x)^{3}=-x^{3}=-g(x)$. 

b) Ví dụ: $y=2x+1, y=(x+2)^{2}, y=x^{2}+x+1$

2. Hàm số tuần hoàn.

HĐ2

a) Đồ thị hàm số trên mỗi đoạn [a ; a + T], [a + T; a + 2T], [a – T; a] có dạng giống nhau.

b) Ta có: f($x_{o}$ + T) = f($x_{o}$)

               f($x_{o}$ - T) = f($x_{o}$)

Định nghĩa: Cho hàm số y = f(x) với tập xác định D. Hàm số y = f(x) được gọi là tuần hoàn nếu tồn tại một số T khác 0 sao cho với mọi x ∈ D, ta có:

• x + T ∈ D và x - T ∈ D.
• f(x + T) = f(x)

Số T nhỏ nhất thỏa mãn (nếu có) các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó.

Ví dụ 2: (SGK – tr.23).

Hướng dẫn giải (SGK – tr.24).

Luyện tập 2

Ví dụ về hàm số tuần hoàn:

Cho T là một số hữu tỉ và hàm số f(x) được cho bởi công thức sau:

• f(x) = 3       nếu x là số hữu tỉ
• f(x) = -3      nếu x là số vô tỉ     

Chứng minh:

f(x) có tập xác định trên R.

• Nếu x là số hữu tỉ thì x + T cũng là số hữu tỉ;
• Nếu x là số vô tỉ thì x + T cũng là số vô tỉ.

Do đó f(x + T) = f(x) với mọi x.

Vậy hàm số f(x) là hàm số tuần hoàn.

Nhận xét: Cho hàm số tuần hoàn chu kì T. Từ đồ thị hàm số đó trên đoạn [a; a + T], ta dịch chuyển song song với trục hoành sang phải (hoặc sang trái) theo đoạn có độ dài T thì được đồ thị hàm số trên đoạn [a + T; a + 2T] (hoặc [a – T; a]).

2. HÀM SỐ Y = SIN X

1. Định nghĩa.

HĐ3

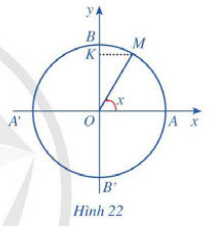
Giả sử tung độ của điểm M là y.

Khi đó ta có sinx = y.

=> Ứng với mỗi số thực x, có duy nhất một giá trị sin x.

Định nghĩa: Quy tắc đặt tương ứng mỗi số thực x với một số thực sin x được gọi là hàm số y = sin x .

Tập xác định của hàm số y = sin x là R.

2. Đồ thị của hàm số y=sin x

HĐ4

a) Thay từng giá trị của x vào hàm số y = sinx ta có bảng sau:

b) Lấy thêm một số điểm (x; sin x) với x ∈ [-π;π]  trong bảng sau và nối lại ta được đồ thị hàm số y = sin x trên đoạn [-π;π].

c) Làm tương tự như trên đối với các đoạn [-3π; -π], [π; 3π],…, ta có đồ thị hàm số y = sin x trên R được biểu diễn ở hình vẽ sau:

3. Tính chất của hàm số y = sin x.

HĐ5

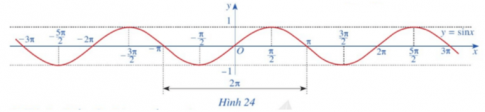
a) Tập giá trị của hàm số y = sin x là [-1; 1].

b) Gốc toạ độ O là tâm đối xứng của đồ thị hàm số.

Do đó hàm số y = sin x là hàm số lẻ.

c) Bằng cách dịch chuyển đồ thị hàm số y = sin x trên đoạn [-π; π] song song với trục hoành sang phải theo đoạn có độ dài 2π, ta sẽ nhận được đồ thị hàm số y = sin x trên đoạn [π; 3π].

Làm tương tự như trên ta sẽ được đồ thị hàm số y = sin x là hàm số tuần hoàn với chu kì T = 2π.

Xét hàm số f(x) = y = sin x trên R, với T = 2π và x ∈ R.

• x + 2π ∈ R và x - 2π ∈ R.
• f(x + 2π) = f(x).

Do đó hàm số y = sinx là hàm số tuần hoàn với chu kì T = 2π.

d) Quan sát đồ thị hàm số y = sin x ta thấy:

• Hàm số đồng biến trên mỗi khoảng $\left ( -\frac{5\pi }{2};\frac{5\pi }{2} \right )$; $\left ( -\frac{\pi }{2};\frac{\pi }{2} \right )$; $\left ( \frac{3\pi }{2};\frac{5\pi }{2} \right )$; ...

Ta có: $\left ( -\frac{5\pi }{2};\frac{5\pi }{2} \right )$ = $\left ( -\frac{\pi }{2}-2\pi ;\frac{\pi }{2}-2\pi  \right )$; $\left ( \frac{3\pi }{2};\frac{5\pi }{2} \right )$ = $\left ( -\frac{\pi }{2}+2\pi ;\frac{\pi }{2}+2\pi  \right )$

Do đó ta có thể viết hàm số đồng biến trên mỗi khoảng $\left ( -\frac{\pi }{2}+k2\pi ;\frac{\pi }{2}+k2\pi  \right )$ với k ∈ Z.

• Hàm số nghịch biến trên mỗi khoảng $\left ( -\frac{7\pi }{2};-\frac{5\pi }{2} \right )$; $\left ( -\frac{3\pi }{2};-\frac{\pi }{2} \right )$; $\left ( \frac{\pi }{2};\frac{3\pi }{2} \right )$; ...

Ta có: $\left ( -\frac{3\pi }{2};-\frac{\pi }{2} \right )$ = $\left ( \frac{\pi }{2}-2\pi ;\frac{3\pi }{2}-2\pi  \right )$; ...

Do đó ta có thể viết hàm số nghịch biến trên mỗi khoảng $\left ( \frac{\pi }{2}+k2\pi ;\frac{3\pi }{2}+k2\pi  \right )$ với k ∈ Z.

Tính chất

• Hàm số y = sin x là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ;
• Hàm số y = sin x tuần hoàn chu kì 2π.
• Hàm số y = sin x đồng biến trên khoảng $\left ( -\frac{\pi }{2}+k2\pi ;\frac{\pi }{2}+k2\pi  \right )$, nghịch biến trên mỗi khoảng $\left ( \frac{\pi }{2}+k2\pi ;\frac{3\pi }{2}+k2\pi  \right )$ với k∈Z.

Ví dụ 3: (SGK – tr.25).

Hướng dẫn giải (SGK – tr.23).

Luyện tập 3

Do $(-\frac{7\pi }{2}; -\frac{5\pi }{2}) = (\frac{\pi }{2}-4\pi ,\frac{3\pi }{2}-4\pi)$ nên hàm số $y=sinx$ nghịch biến trên khoảng $(-\frac{7\pi }{2}; -\frac{5\pi }{2})$. 

Nhận xét: Dựa vào đồ thị của hàm số y = sin x (hình 24), ta thấy sin x = 0 tại những giá trị x = kπ, (k ∈ Z). Vì vậy, tập hợp các số thực x sao cho sin x ≠ 0 là E = R\ k ∈ Z. 

3. HÀM SỐ Y = COS X

1. Định nghĩa

HĐ6

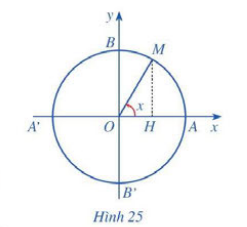
Giả sử hoành độ của điểm M là y.

Khi đó ta có cos x = y => Ứng với mỗi số thực x, có duy nhất một giá trị cos x.

Định nghĩa: Quy tắc đặt tương ứng mỗi số thực x với một số thực cos x được gọi là hàm số y = cos x.

Tập xác định của hàm số y = cos x là R.

2. Đồ thị của hàm số y=cos x.

HĐ7

a) Thay từng giá trị của x vào hàm số y = cos x ta có bảng sau:

b) Lấy thêm một số điểm (x; cos x ) với x ∈ [-π; π]  trong bảng sau và nối lại ta được đồ thị hàm số y = cos x trên đoạn [-π; π].

c) Làm tương tự như trên đối với các đoạn [-3π; -π], [π; 3π],…, ta có đồ thị hàm số y = cos x trên R được biểu diễn ở hình vẽ sau:

3. Tính chất của hàm số y = cos x.

HĐ8

a) Tập giá trị của hàm số y = cos x là [‒1; 1].

b) Trục tung là trục đối xứng của đồ thị hàm số.

Do đó hàm số y = cos x là hàm số chẵn.

c) Bằng cách dịch chuyển đồ thị hàm số y = cos x trên đoạn [‒π; π] song song với trục hoành sang phải theo đoạn có độ dài 2π, ta sẽ nhận được đồ thị hàm số y = cos x trên đoạn [π; 3π].

Làm tương tự như trên ta sẽ được đồ thị hàm số y = cosx trên ℝ.

Xét hàm số f(x) = y = cos x trên ℝ, với T = 2π và x ∈ R ta có:

• x + 2π ∈ R và x – 2π ∈ R;
• f(x + 2π) = f(x)

Do đó hàm số y = cos x là hàm số tuần hoàn với chu kì T = 2π.

d) Quan sát đồ thị hàm số y = cosx ta thấy:

• Hàm số đồng biến trên mỗi khoảng (‒3π; ‒2π); (‒π; 0); (π; 2π); …

Ta có: (‒3π;‒2π) = (‒π ‒2π; 0 ‒ 2π);

(π; 2π) = (‒π + 2π; 0 + 2π); …

Do đó ta có thể viết hàm số đồng biến trên mỗi khoảng (‒π + k2π; k2π) với k ∈ Z.

• Hàm số nghịch biến trên mỗi khoảng (‒2π; ‒π); (0; π); (2π; 3π); …

Ta có: (‒2π; ‒π) = (0 ‒ 2π; π ‒ 2π);

(2π; 3π) = (0 + 2π; π + 2π);  

Do đó ta có thể viết hàm số nghịch biến trên mỗi khoảng (k2π; π + k2π) với k∈Z.

Tính chất

• Hàm số y = cos x là hàm số chẵn, có đồ thị đối xứng qua trục tung.
• Hàm số y = cos x tuần hoàn chu kì 2π.
• Hàm số y = cos x đồng biến trên mỗi khoảng [-π+k2π; k2π], nghịch biến trên mỗi khoảng [k2π; π+k2π] với k ∈ Z.

Ví dụ 4: (SGK – tr.27).

Hướng dẫn giải (SGK – tr.27).

Luyện tập 4

Do $(-2\pi ;-\pi )=(-\pi -\pi ;-\pi )$ nên hàm số $y=cosx$ đồng biến trên khoảng $(-2\pi ;-\pi )$. 

4. HÀM SỐ Y = TAN X

1. Định nghĩa

HĐ9

Nếu cos x ≠ 0, tức x ∈ R\ {$\frac{\pi }{2}+k\pi $ | k ∈ Z}

Hay x ∈ D thì ta có: tan x = $\frac{sinx}{cosx}$.

Định nghĩa

• Quy tắc đặt tương ứng mỗi số thực x ∈ D với một số thực tan x được gọi là hàm số y = tan x .
• Tập xác định của hàm số y=tan x là D = R\ {$\frac{\pi }{2}+k\pi $ | k ∈ Z}

2. Đồ thị hàm số y=tan x

HĐ10

a) Thay từng giá trị của x vào hàm số y = tanx ta có bảng sau:

b) Lấy thêm một số điểm x;tan x với x ∈ $\left ( -\frac{\pi }{2};\frac{\pi }{2} \right )$ trong bảng sau và nối lại ta được đồ thị hàm số y = tanx trên khoảng x ∈ $\left ( -\frac{\pi }{2};\frac{\pi }{2} \right )$

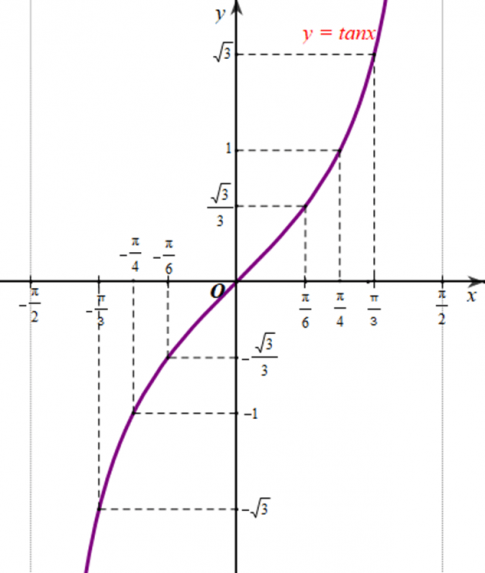
c) Làm tương tự như trên đối với các $\left ( \frac{\pi }{2};\frac{3\pi }{2} \right )$, $\left ( -\frac{3\pi }{2};-\frac{\pi }{2} \right )$,… ta có đồ thị hàm số y = tanx trên D được biểu diễn ở hình vẽ sau:

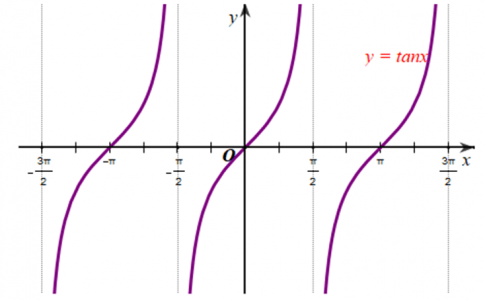
3. Tính chất của hàm số y = tan x

HĐ11

a) Tập giá trị của hàm số y = tan x là R.

b) Gốc toạ độ là tâm đối xứng của đồ thị hàm số y = tanx.

Do đó hàm số y = tan x là hàm số lẻ.

c) Bằng cách dịch chuyển đồ thị hàm số y = tan x trên khoảng $\left ( -\frac{\pi }{2};\frac{\pi }{2} \right )$ song song với trục hoành sang phải theo đoạn có độ dài π, ta sẽ nhận được đồ thị hàm số y = tan x trên khoảng $\left ( \frac{\pi }{2};\frac{3\pi }{2} \right )$.

Làm tương tự như trên ta sẽ được đồ thị hàm số y = tan x trên R\ {$\frac{\pi }{2}+k\pi $ | k ∈ Z}.

Xét hàm số f(x) = y = tanx trên D=R\ k∈Z với T = π và x ∈ D ta có:

• x + π ∈ D và x - π ∈ D.
• f(x + π) = f(x).

Do đó hàm số y = tan x là hàm số tuần hoàn với chu kì T = π.

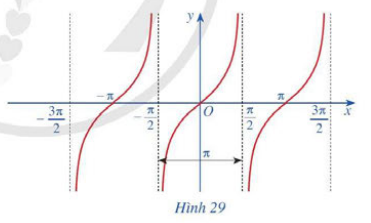
d) Quan sát đồ thị hàm số y = tanx ở Hình 29, ta thấy: đồ thị hàm số đồng biến trên mỗi khoảng $\left ( -\frac{3\pi }{2};-\frac{\pi }{2} \right )$, $\left ( -\frac{\pi }{2};\frac{\pi }{2} \right )$, $\left ( \frac{\pi }{2};\frac{3\pi }{2} \right )$, ...

Ta có: $\left ( -\frac{\pi }{2};\frac{\pi }{2} \right )$ = $\left ( -\frac{\pi }{2}+\pi ;\frac{\pi }{2}+\pi  \right )$

Do đó ta có thể viết đồ thị hàm số y = tan x đồng biến trên mỗi khoảng $\left ( -\frac{\pi }{2}+k\pi ;\frac{\pi }{2}+k\pi  \right )$ với k ∈ Z.

Tính chất

• Hàm số y = tan x là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O;
• Hàm số y = tan x tuần hoàn chu kì π.
• Hàm số y = tan x đồng biến trên mỗi khoảng $\left ( -\frac{\pi }{2}+k\pi ;\frac{\pi }{2}+k\pi  \right )$ với k ∈ Z.

Ví dụ 5: (SGK – tr.29).

Hướng dẫn giải (SGK – tr.29).

Luyện tập 5

Với mỗi số thực m, chỉ có một giao điểm giữa đường thẳng $y = m $ và đồ thị hàm số $y=tanx$ trên khoảng $(-\frac{\pi }{2};\frac{\pi }{2})$. 

5. HÀM SỐ Y = COT X

1. Định nghĩa

HĐ12

Nếu sin x ≠ 0, tức x ∈ R\ {$k\pi $ | k ∈ Z} hay xE thì ta có: cotx = $\frac{cosx}{sinx}$.

Định nghĩa

Quy tắc đặt tương ứng mỗi số thực x ∈ E với một số thực cotx được gọi là hàm số y = cot x .

Tập xác định của hàm số y = cotx là E = R\ {$k\pi $ | k ∈ Z}.

2. Đồ thị của hàm số y = cot x.

HĐ13

a) Thay từng giá trị của x vào hàm số y = cotx ta có bảng sau:

b) Lấy thêm một số điểm (x; cot x) với x ∈ (0; π) trong bảng sau và nối lại ta được đồ thị hàm số y = cot x trên khoảng x ∈ (0; π)

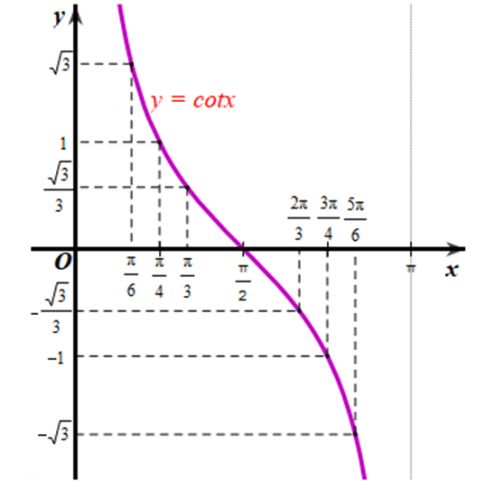
c)  Làm tương tự như trên đối với các $\left ( \frac{\pi }{2};\frac{3\pi }{2} \right )$, $\left ( -\frac{3\pi }{2};-\frac{\pi }{2} \right )$,…, ta có đồ thị hàm số y = tan x trên D được biểu diễn ở hình vẽ sau:

3. Tính chất của hàm số y = cot x

HĐ14

a) Tập giá trị của hàm số y = cot x là ℝ.

b) Gốc toạ độ là tâm đối xứng của đồ thị hàm số y = cotx .

Do đó hàm số y = cot x là hàm số lẻ.

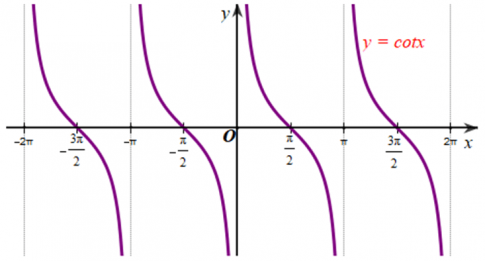
c) Bằng cách dịch chuyển đồ thị hàm số y = cot x trên khoảng (0; π) song song với trục hoành sang phải theo đoạn có độ dài π, ta sẽ nhận được đồ thị hàm số y = cot x trên khoảng (π; 2π).

Làm tương tự như trên ta sẽ được đồ thị hàm số y = cotx trên R\ {kπ | k∈Z}.

Xét hàm số f(x) = y = cot x trên D = R\ {kπ | k∈Z}, với T = π và x ∈ D.

• x + π ∈ D và x - π ∈ D.
• f(x + π) = f(x).

Do đó hàm số y = cotx  là hàm số tuần hoàn với chu kì T = π.

d) Quan sát đồ thị hàm số y = cot x ở Hình 31, ta thấy: đồ thị hàm số nghịch biến trên mỗi khoảng (-2π; -π); (-π; 0); (0; π); (π; 2π),…

Ta có thể viết đồ thị hàm số y = cotx nghịch biến trên mỗi khoảng (kπ; π + kπ) với k ∈ Z.

Tính chất

• Hàm số y = cotx là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O.
• Hàm số y = cotx tuần hoàn chu kì π.
• Hàm số y = cotx  nghịch biến trên mỗi khoảng (kπ; π + kπ) với k ∈ Z.

Ví dụ 6: (SGK – tr.30).

Hướng dẫn giải (SGK – tr.30).

Luyện tập 6

Xét đồ thị của hàm số y = m và đồ thị của hàm số y = cotx trên khoảng (0; π) (hình vẽ).

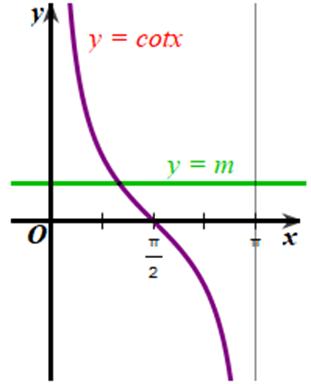
Từ đồ thị của hai hàm số trên hình vẽ, ta thấy mọi m ∈ R thì hai đồ thị trên luôn cắt nhau tại 1 điểm.

Vậy số giao điểm của đường thẳng y = m (m ∈ ℝ) và đồ thị hàm số y = cotx trên khoảng (0; π) là 1