I. PHÉP TOÁN TRÊN CÁC BIẾN CỐ

1. Biến cố hợp

HĐ1

a) A = {2; 4; 6},  B = {3; 6}

b) Biến cố C là “Mặt xuất hiện của xúc xắc có số chấm là số chẵn hoặc chia hết cho 3”

Khái niệm: Cho hai biến cố A và B. Khi đó A, B là các tập con của không gian mẫu Ω. Đặt C = A ∪ B, ta có C là một biến cố và được gọi là biến cố hợp của hai biến cố A và B, kí hiệu A ∪ B.

Chú ý: Xét một kết quả thuận lợi α  cho biến cố C, tức là α ∈ C. 

Vì C = A ∪ B nên α ∈ A hoặc α ∈ B. Tức là biến cố A hoặc biến cố B xảy ra. 

Vì vậy, biến cố C có thể phát biểu là “A xảy ra hoặc B xảy ra ” hay “Có ít nhất một trong các biến cố A, B xảy ra”.

Ví dụ 1: (SGK – tr.16)

Hướng dẫn giải (SGK – tr.16)

Luyện tập 1

Ta có:

A = {3; 6; 9; 12} và B = {4; 8; 12}

A ∪ B = C. Vậy biến cố C là “Số thẻ rút được là số chia hết cho 3 hoặc 4”.

2. Biến cố giao

HĐ2

Ta có: D = {6}

Biến cố D “Mặt 6 chấm xuất hiện ở cả biến cố A và biến cố B”.

Định nghĩa: Cho hai biến cố A và B. Khi đó A, B là các tập hợp con của không gian mẫu Ω. Đặt D = A ∩ B, ta có D là một biến cố và được gọi là biến cố giao của hai biến cố A và B, kí hiệu à A ∩ B hay AB.

Chú ý: Xét một kết quả thuận lợi β cho biến cố D, tức là β ∈ D. 

Vì D = A ∩ B nên β ∈ A và β ∈ B. Nghĩa là cả hai biến cố A và B cùng xảy ra. 

Vì vậy, biến cố D có thể phát biểu là “Cả A và B cùng xảy ra”. 

Ví dụ 2: (SGK – tr.17)

Hướng dẫn giải (SGK – tr.17)

Luyện tập 2

Ta có: A = {1; 3; 5}; B = {1; 3; 5}.

Biến cố A ∩ B “Số chấm xuất hiện ở cả hai lần gieo là số lẻ”.

3. Biến cố xung khắc

HĐ3

Ta có: A = {1; 3; 5}; B = {2; 4; 6}

=> A ∩ B = ∅ 

Định nghĩa: Cho hai biến cố A và B. Khi đó A, B là các tập con của không gian mẫu Ω. Nếu A ∩ B = ∅ thì A và B gọi là biến cố xung khắc.

Chú ý: Xét một kết quả thuận lợi γ cho biến cố A, tức là γ ∈ A. Vì A ∩ B = ∅ nên B, tức là không là một kết quả thuận lợi cho biến cố B. Do đó, hai biến cố A và B xung khắc khi và chỉ khi nếu biến cố này xảy ra thì biến cố kia không xảy ra.

Ví dụ 3: (SGK – tr.17)

Hướng dẫn giải (SGK – tr.18)

Luyện tập 3

Biến cố A xung khắc biến cố B.

II. BIẾN CỐ ĐỘC LẬP

HĐ4

Một kết quả thuận lợi cho biến cố A là xuất hiện mặt S ở lần tung thứ nhất (xác suất là $\frac{1}{2}$).

Một kết quả thuận lợi cho biến cố B là xuất hiện mặt N ở lần tung thứ hai (xác suất là $\frac{1}{2}$).

=> Kết quả thuận lợi cho biến cố A không ảnh hưởng gì đến xác xuất xảy ra của biến cố B.

Định nghĩa: Cho hai biến cố A và B. Hai biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng đến xác suất xảy ra của biến cố kia.

Chú ý: Nếu A, B là hai biến cố độc lập thì mỗi cặp biến cố sau cũng độc lập: A và B; A và B; A và B.

Ví dụ 4: (SGK – tr.18)

Hướng dẫn giải (SGK – tr.19)

Luyện tập 4

Ta có: A = {2; 3; 5}; B= {4; 6} 

• Khi biến cố A xảy ra hay không xảy ra thì xác suất của biến cố B đều là $\frac{2}{6}=\frac{1}{3}$
• Khi biến cố B xảy ra hay không xảy ra thì xác suất của biến cố A đều là $\frac{3}{6}=\frac{1}{2}$

=> Biến cố A và B độc lập với nhau.

Biến cố A và B không xung khắc, vì có kết quả thỏa mãn của A và B.

Kết quả (3; 6) là kết quả thuận lợi cho cả hai biến cố A và B. Do đó A ∩ B ≠ ∅. 

Vậy A và B không xung khắc

III. QUY TẮC TÍNH XÁC SUẤT

1. Công thức cộng xác suất

HĐ5

a) Có A = {2; 4; 6; 8; 10; 12; 14; 16; 18; 20}, B={7; 14}

$P(A)=\frac{10}{20}=\frac{1}{2}$

$P(B)=\frac{2}{20}=\frac{1}{10}$

=> $P(A\cap B)=\frac{1}{20}$

$P(A\cup B)=\frac{11}{20}$

b) Có $P(A\cup B)=P(A)+P(B)- P(A\cap B)$ Vì $\frac{1}{2}+\frac{1}{10}-\frac{1}{20}=\frac{11}{20}$

Định lí

• Cho hai biến cố A và B. Khi đó P(A ∪ B) = P(A) + P(B) - P(A ∩ B).
• Nếu hai biến cố A và B là xung khắc thì A ∩ B = ∅, suy ra P(A ∩ B) = 0. Vì thế, ta có hệ quả như sau:

Hệ quả: Nếu hai biến cố A và B xung khắc thì P(A ∪ B) = P(A) + P(B)

Ví dụ 5: (SGK – tr.19)

Hướng dẫn giải (SGk – tr.19)

Ví dụ 6: (SGK – tr.20)

Hướng dẫn giải (SGK – tr.20)

Luyện tập 5

Có A = {7, 14, 21, 28, 35, 42, 49}; B = {11, 22, 33, 44}

=>  $A\cap B $ = ∅

Đây là hai biến cố xung khắc

=> $P(A\cup B)=P(A)+P(B)=\frac{7}{52}+\frac{4}{52}=\frac{11}{52}$

2. Công thức nhân xác suất

HĐ6

a) Có $P(A)=\frac{3}{7}$

$P(B)=\frac{4}{7}$

$P(A\cap B)=\frac{12}{49}$

b) Ta thấy $P(A\cap B)=\frac{3}{7}.\frac{4}{7}=\frac{12}{49}=P(A).P(B)$

Định lí: Cho hai biến cố A và B

Nếu hai biến cố A và B là độc lập thì P(A ∩ B) = P(A).P(B)

Chú ý: Nếu P(A ∩ B) ≠ P(A).P(B) thì hai biến cố A và B không độc lập.

Ví dụ 7: (SGK – tr.20)

Hướng dẫn giải (SGK – tr.20)

Luyện tập 6

Theo đề bài, ta thấy hai biến cố A và B là hai biến cố độc lập

$P(C)=P(A).P(B)=0,8.0,9=0,72$

Ví dụ 8: (SGK – tr.21)

Hướng dẫn giải (SGk – tr.21)

IV. TÍNH XÁC SUẤT CỦA BIẾN CỐ TRONG MỘT SỐ BÀI TOÁN ĐƠN GIẢN

1. Tính xác suất của biến cố bằng phương pháp tổ hợp

Ví dụ 9: (SGK – tr.21)

Hướng dẫn giải (SGK – tr.21+22)

Luyện tập 7

Xét các biến cố 

H: "Ba đỉnh của tam giác là 3 điểm của cả hai đường thẳng $d_{1}$ và $d_{2}$"

A: "Trong ba đỉnh của tam giác có 1 điểm thuộc $d_{1}$, 2 điểm thuộc $d_{2}$"

B: "Trong ba đỉnh của tam giác có 2 điểm thuộc $d_{1}$, 1 điểm thuộc $d_{2}$"

Do hai biến cố A và B xung khắc nên:

$n(H)=n(A)+n(B)$

Số các kết quả thuận lợi cho biến cố A là: 

$n(A)=C_{1}^{17}\cdot C_{2}^{20}=3230$ 

Số các kết quả thuận lợi cho biến cố B là:

$n(B)=C_{2}^{17}\cdot C_{1}^{20}=2720$ 

Số các kết quả thuận lợi cho biến cố H là 

$n(H)=n(A)+n(B)=3230+2720=5950$ 

Có n(Ω)=$C_{3}^{37}=7770 $

=>$P(H) = \frac{5950}{7770}=\frac{85}{111}$

2. Tính xác suất của biến cố bằng cách sử dụng sơ đồ hình cây

HĐ7

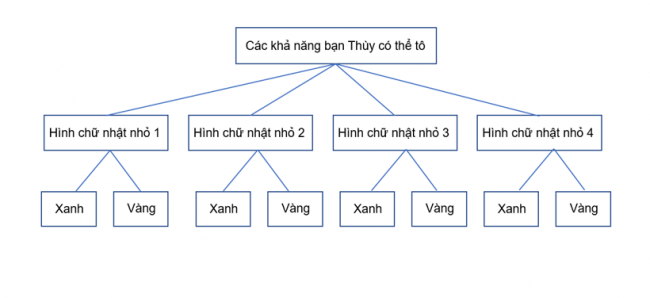
Ví dụ 10: (SGK – tr.23)

Hướng dẫn giải (SGK – tr.23)

Luyện tập 8

Có n(Ω) = $C^{18}_{5}$ = 8568 

Xét biến cố A: "Trong 5 viên bi có 1 viên bi màu xanh, 2 viên bi màu vàng, 2 viên bi màu đỏ"

$n(A)=C_{1}^{5}\cdot C_{2}^{6}\cdot C_{2}^{7}=1575$

Xét biến cố B: "Trong 5 viên bi có 3 viên bi màu xanh, 1 viên bi màu vàng, 1 viên bi màu đỏ"

$n(B)=C_{3}^{5}\cdot C_{1}^{6}\cdot C_{1}^{7}=420$

Vậy xác suất để 5 viên bi được chọn có đủ 3 màu và số bi màu đỏ bằng số bi màu vàng là: $\frac{1575+420}{8568}=\frac{95}{408}$