Lý thuyết trọng tâm toán 10 cánh diều bài 2: Tập hợp. Các phép toán trên tập hợp
Tổng hợp kiến thức trọng tâm toán 10 cánh diều bài 2: Tập hợp. Các phép toán trên tập hợp. Tài liệu nhằm củng cố, ôn tập lại nội dung kiến thức bài học cho học sinh dễ nhớ, dễ ôn luyện. Kéo xuống để tham khảo
I. TẬP HỢP
HĐ1.
Có hai cách cho một tập hợp:
+ Liệt kê các phần tử của tập hợp;
Chẳng hạn: A = {0; 1; 2; 3; 4; 5}
+ Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Chẳng hạn: A = {x ∈ N|0 ≤ x ≤5}
HĐ2.
a) A = {a; b; c}.
b) d ∉ A
Ví dụ 1 (SGK – tr12)
HĐ3.
+ C = {x ∈ ℝ | $x^2 < 0$}
Ta có với mọi số thực x thì $x^2 ≥ 0$, suy ra không tồn tại số thực x để $x^2 < 0$.
Vậy tập hợp C không có phần tử nào.
+ D = {a}
Tập hợp D có 1 phần tử, là phần tử a.
+ E = {b; c; d}
Tập hợp E có 3 phần tử.
+ ℕ= {0; 1; 2; …}.
Tập hợp ℕ là tập hợp các số tự nhiên. Tập hợp này có vô số phần tử.
Nhận xét:
- Tập hợp không chứa phần tử nào được gọi là tập hợp rỗng (tập rỗng), kí hiệu Ø.
- Một tập hợp có thể không có phân tử nào, cũng có thể có một phần tử, có nhiều phần tử, có vô số phần tử.
Chú ý: Khi tập hợp C là tập hợp rỗng, ta viết C= Ø và không được viết là C= { Ø }.
Luyện tập 1:
+ G ={x ∈ Z| $x^2 −2 = 0$}.
Tập hợp G không chứa phần tử nào vì:
$x^2 −2 = 0$ ⇔ $x = ±\sqrt{2}$ ∉ Z.
+ N*={1;2;3;..}.
Tập hợp N* có vô số phần tử.
II. TẬP CON VÀ TẬP HỢP BẰNG NHAU.
Tập con
HĐ4.
a) A = {−2; −1; 0; 1; 2}
B={−3; −2; −1; 0; 1; 2; 3}
b) Mỗi phần tử của tập hợp A đều thuộc tập hợp B.
Kết luận:
Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là môt tập hợp con của B và viết là A ⸦ B. Ta còn đọc A chứa trong B.
Quy ước: Tập hợp Ø được coi là tập hợp con của mọi tập hợp.
Chú ý:
+ A ⊂ B ⇔ (∀x, x∈A ⇒ x∈B)
+ Khi A ⊂ B, ta cũng có thể viết B ⸧ A
+ Nếu A không phải tập hợp con của B, ta viết A ⊄ B.
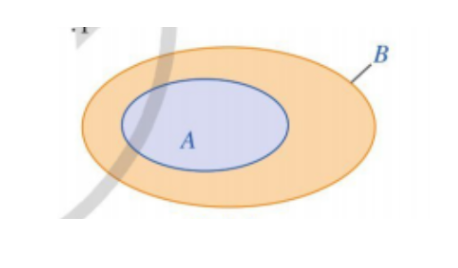
Ví dụ 2 (SGK – tr13)
Luyện tập 2:
Lấy n bất kì thuộc tập hợp B.
Ta có: n chia hết cho 9
n đều viết được dưới dạng:
n = 9k (k∈ N)
⇒ n = 3.(3k) ⋮ 3 (k ∈ N)
⇒ n ∈ A
Như vậy, mọi phần tử của tập hợp B đều là phần tử của tập hợp A hay B ⸦ A.
Kết luận:
Ta có các tính chất sau:
- A ⸦ A với mọi tập hợp A
- Nếu A ⸦ B và B ⸦ C thì A ⸦ C
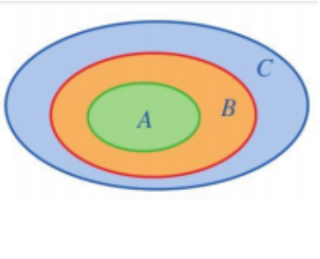
Tập hợp băng nhau
HĐ5.
Ta có: B = {0;6;12;18}
a) Tất cả các phần tử của tập A đều thuộc tập B nên A⊂B là mệnh đề đúng.
b) Tất cả các phần tử của tập B đều thuộc tập A nên B⊂A là mệnh đề đúng.
Kết luận:
Khi A ⸦ B và B ⸦ A thì ta nói hai tập hợp A và B bằng nhau, viết là A = B.
Chú ý:
A = B ⇔ (Ɐ x, x ∈ A ⇔ x ∈ B).
Ví dụ 3 (SGK -tr14)
Luyện tập 3.
Ta có:
n chia hết cho 3 và 4 khi và chỉ khi n chia hết cho 12 do (3, 4) =1.
Vậy E = G.
III. GIAO CỦA HAI TẬP HỢP
HĐ6.
Danh sách các bạn đăng kí tham gia cả hai câu lạc bộ là: An, Chung.
Kết luận:
Tập hợp gồm tất cả các phần tử vừa thuộc tập hợp A vừa thuộc tập hợp B được gọi là giao của hai tập hợp A và B.
Kí hiệu là A ∩ B.
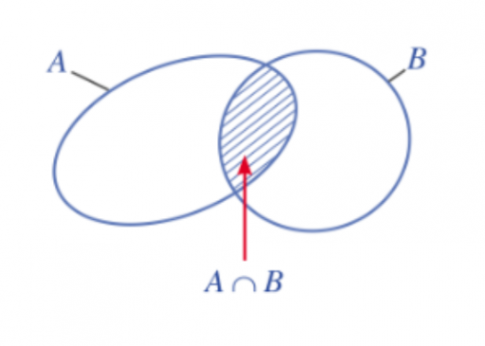
Lưu ý:
x ∈ A ∩ B khi và chỉ khi x ∈ A và x ∈ B.
Ví dụ 4 (SGK -tr14)
IV. HỢP CỦA HAI TẬP HỢP
HĐ7.
Danh sách những môn thi đấu mà cả hai trường đã đề xuất là: Bóng bàn, Bóng đá, Bóng rổ, Cầu lông.
Kết luận:
Tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc tập hợp B được gọi là hợp của hai tập hợp A và B. Kí hiệu là A ∪ B.
Chú ý: x ∈ A ∪ B. khi và chỉ khi x ∈ A và x ∈ B
Ví dụ 5 (SGK -tr15)
Luyện tập 4.
A ∩ B={0}
A ∪ B=R
V. PHẦN BÙ. HIỆU CỦA HAI TẬP HỢP
HĐ8.
Tập hợp những số thực không phải là số vô tỉ chính là tập hợp Q các số hữu tỉ.
Kết luận:
Cho tập hợp A là tập hợp con của tập hợp B. Tập hợp những phân tử thuộc B mà không thuộc A được gọi là phần bù của A trong B, kí hiệu là $C_{B}A$.
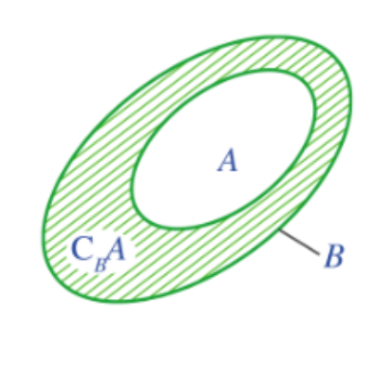
Ví dụ 6 (SGK tr16)
HĐ9
Các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B là: 2; 14.
Kết luận:
Tập hợp gồm các phần tử thuộc A nhưng không thuộc B được gọi là hiệu của A và B kí hiệu là A \ B.
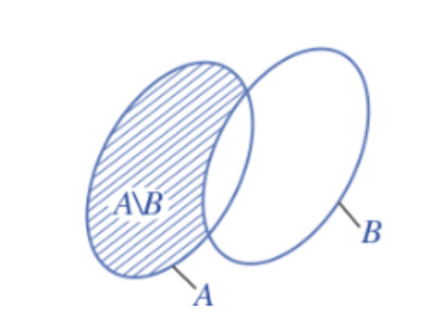
Lưu ý:
+ x ∈ A \ B khi và chỉ khi x ∈ A và x ∉ B
+ Nếu B ⊂ A thì A \ B = $C_{A}B$
Ví dụ 7 (SGK – tr16)
Ví dụ 8 (SGK – tr16)
Luyện tập 5:
Ta có:
A={ x ∈ Z| −2 ≤ x ≤ 3}= {−2; −1; 0; 1; 2; 3}
Và B= { x ∈ R| $x^2 - x - 6=0$} = { −2; 3}
Khi đó:
Tập hợp A∖B gồm các phần tử thuộc A mà không thuộc B. Vậy A∖B={−1; 0; 1; 2}.
Tập hợp B∖A gồm các phần tử thuộc B mà không thuộc A. Vậy B∖A= ∅
VI. CÁC TẬP HỢP SỐ
Các tập hợp số đã học
Mối quan hệ giữa các tập hợp số: N ⊂ Z ⊂ Q ⊂ R.
2. Một số tập con thường dùng của tập hợp số thực
Cho a và b là hai số thực với a < b.
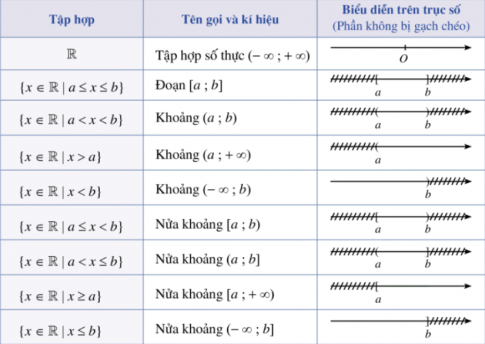
Ví dụ 9 (SGK -tr18)
Bình luận