Bài giảng điện tử toán 11 chân trời sáng tạo

CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI HỌC HÔM NAY!

KHỞI ĐỘNG

• Tình huống mở đầu:
• Nhắc lại khái niệm số thập phân vô hạn tuần hoàn?

Số thập phân vô hạn tuần hoàn: Trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi

Theo em bạn nào nói đúng? Tại sao?

SOẠN TOÁN 10 CTST SOẠN CHI TIẾT:

• Bài giảng Powerpoint toán 10 chân trời sáng tạo
• Tải GA word toán 10 chân trời sáng tạo
• Tải GA dạy thêm toán 10 chân trời sáng tạo

CHƯƠNG III: GIỚI HẠN. HÀM SỐ LIÊN TỤC

BÀI 1: GIỚI HẠN CỦA DÃY SỐ

NỘI DUNG BÀI HỌC

1. GIỚI HẠN HỮU HẠN CỦA DÃY SỐ
2. a) Giới hạn 0 của dãy số

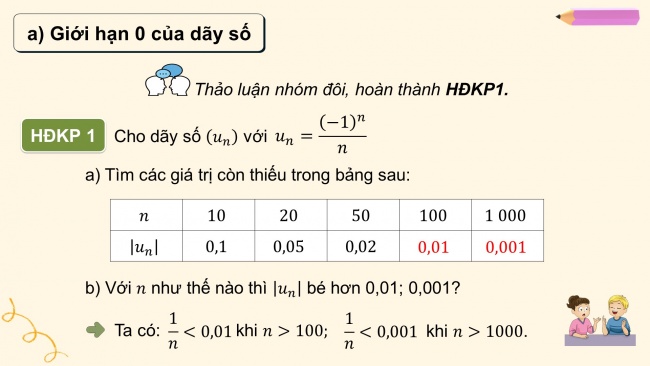
Thảo luận nhóm đôi, hoàn thành HĐKP1.

                  Cho dãy số  với

1. a) Tìm các giá trị còn thiếu trong bảng sau:

1. b) Với như thế nào thì bé hơn 0,01; 0,001?

Ta có:                khi

khi .

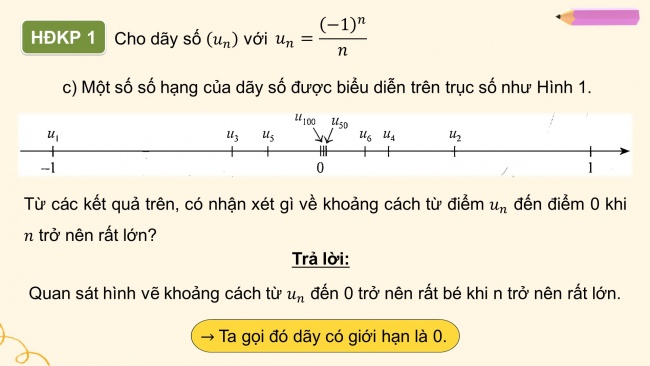
HDKP 1:                   Cho dãy số  với

1. c) Một số số hạng của dãy số được biểu diễn trên trục số như Hình 1.

Từ các kết quả trên, có nhận xét gì về khoảng cách từ điểm  đến điểm 0 khi  trở nên rất lớn?

Trả lời:

Quan sát hình vẽ khoảng cách từ  đến 0 trở nên rất bé khi n trở nên rất lớn.Ta gọi đó dãy có giới hạn là 0.

KẾT LUẬN

Ta nói dãy số  có giới hạn 0 khi  dần tới dương vô cực, nếu  nhỏ hơn một số dương bất kì cho trước, kể từ một số hạng nào đó trở đi, kí hiệu  hay  khi .

Ta còn viết là .

Ví dụ 1

Với dãy số  

                  ở HĐKP 1, sử dụng định nghĩa, chứng tỏ rằng lim .

Giải

Với số thực dương  bé tuỳ ý cho trước, lấy số tự nhiên  sao cho . Khi đó, với mọi số tự nhiên  sao cho , ta có

Theo định nghĩa, .

Thảo luận nhóm đôi, trả lời câu hỏi.

1. Hãy so sánh với (với k nguyên dương). Từ đó có thể kết luận gì về giá trị       ?

Ta thấy

Từ đó

2. Xét các dãy số có dạng với . Khi n càng lớn thì giá trị sẽ như thế nào? Từ đó xác định giá trị 

Khi n càng lớn thì giá trị  càng nhỏ.

SOẠN TOÁN 11 CTST CHUẨN KHÁC:

• Giáo án toán 11 mới năm 2023 chân trời sáng tạo
  Giáo án chuyên đề toán 11 mới năm 2023 chân trời sáng tạo
• Giáo án dạy thêm toán 11 mới năm 2023 chân trời sáng tạo

Giới hạn cơ bản:

• , với  nguyên dương bất kì.
• , với là số thực thoả mãn .

Ví dụ 2: Áp dụng giới hạn cơ bản, tìm

Giải

Ta có:

Do đó

Nên

Thực hành 1:

Thảo luận nhóm đôi, hoàn thành Thực hành 1.

Tìm các giới hạn sau:

Giải

1. a) vì                  , với  nguyên dương bất kì.
2. b) vì , với là số thực thoả mãn  trong trường hợp này
3. b) Giới hạn hữu hạn của dãy số

Thảo luận nhóm đôi, hoàn thành HĐKP2.

Cho dãy số  với

1. a) Cho dãy số với . Tìm giới hạn .
2. b) Biểu diễn các điểm trên trục số. Có nhận xét gì về vị trí của các điểm khi n trở nên rất lớn?

Giải

Ta có:

Nhận xét: Điểm  càng dần đến điểm 2 khi n trở nên rất lớn.

KẾT LUẬN

Ta nói dãy số  có giới hạn hũu hạn là số  (hay  dần tới ) khi  dần tới dương vô cực, nếu lim . Khi đó, ta viết  hay  hay  khi .

Chú ý: Nếu  là hằng số) thì .

Ví dụ 3: Dùng định nghĩa, tìm giới hạn

Giải

Đặt

Ta có

Hay

Suy ra

Theo định nghĩa

Vậy

Thực hành 2:

Tìm các giới hạn sau:

Giải

1. a) , suy ra .
2. b) , suy ra .
3. CÁC PHÉP TOÁN VỀ GIỚI HẠN CỦA DÃY SỐ

Thảo luận nhóm đôi, hoàn thành HĐKP3.

SOẠN GIÁO ÁN TẤT CẢ CÁC MÔN LỚP 11 MỚI:

• Giáo án tất cả các môn lớp 11 chân trời sáng tạo
• Giáo án tất cả các môn lớp 11 cánh diều
• Giáo án tất cả các môn lớp 11 kết nối tri thức

HĐKP 3:

Ở trên ta biết

1. a) Tìm các giới hạn và
2. b) Từ đó, nêu nhận xét về và

Giải

KẾT LUẬN

Cho  và  là hằng số. Khi đó:

• Nếu thi  và

Ví dụ 4:

Tìm các giới hạn sau:

Giải

1. a) Ta có

(chia cả tử và mẫu cho )

Từ đó

Ví dụ 4

Tìm các giới hạn sau:

Ta có

Thực hành 3:

Tìm các giới hạn sau:

.

3. TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN

Thảo luận nhóm bốn, hoàn thành HĐKP4.

                 Từ một hình vuông có cạnh bằng 1, tô màu của một nửa hình vuông, rồi to màu một nữa hình còn lại, và cứ tiếp tục như vậy (xem Hình 2).

1. a) Xác định diện tích của phần hình được tô màu lần thứ
2. b) Tính tổng của phần hình được tô màu sau lần to thứ
3. c) Tìm giới hạn lim và so sánh giới hạn này với diện tích hình vuông ban đầu.

---------------Còn tiếp-------------------