Lời giải bài số 20, 21, 28 Đề thi thử THPT quốc gia môn toán năm 2017 của trường THPT Hà Huy Tập lần 1
HƯỚNG DẪN GIẢI
Câu 20: Tìm tất cả các giá trị của tham số m để phương trình $4(\log_{2} \sqrt{2})^{2}-\log_{\frac{1}{2}} x +m=0$ có nghiệm thuộc khoảng $(0,1)$.
| A. $m \in (-\infty,0]$. | B. $m \in (0,\frac{1}{4}]$. | C. $m\in [\frac{1}{4},+\infty)$. | D. $m \in (-\infty, \frac{1}{4}]$. |
Giải: Đáp án D
Tập xác định $D=(0,+\infty)$.
Ta có $4(\log_{2} \sqrt{2})^{2}-\log_{\frac{1}{2}} x +m=0 \Leftrightarrow (\log_{2} x)^{2}+\log_{2} x+m=0$.
Đặt $t=\log_{2}(x)$. Do $x \in (0,1)$ nên $t<0$. Bài toán trở thành tìm m để $t^{2}+t+m=0$ có ít nhất một nghiệm $t<0$.
Đặt $f(t)=t^{2}+ \Rightarrow f'(t)=2t+1=0 \Leftrightarrow t=-\frac{1}{2}$. Ta có bảng biến thiên

Để phương trình $t^{2}+t=-m$ có ít nhất một nghiệm $t<0$ thì $-m \geq -\frac{1}{4} \Leftrightarrow m \leq \frac{1}{4}$.
Câu 21: Sự tăng trưởng của loại vi khuẩn tuân theo công thức $S=A.e^{rt}$, trong đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng (r>0), t là thời gian tăng trưởng (tính theo đơn vị là giờ). Biết số vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Thời gian để vi khuẩn tăng gấp đôi số ban đầu gần đúng nhất với kết quả nào sau đây?
| A. 3 giờ 20 phút. | B. 3 giờ 9 phút. | C. 3 giờ 40 phút. | D. 3 giờ 2 phút. |
Giải: Đáp án B
Ta có $300=100. e^{5r}\Leftrightarrow e^{5r}=3\Leftrightarrow 5r=\ln 3\Leftrightarrow r=\frac{\ln 3}{5}.$
Gọi thời gian cần tìm là t. Theo yêu cầu của bài toán ta có $200=100.e^{rt}\Leftrightarrow e^{rt}=2\Leftrightarrow rt=\ln 2\Leftrightarrow t=\frac{5 \ln 2}{\ln 3} \approx 3,15$(h).
Vậy t=3 giờ 9 phút.
Câu 28: Một sân chơi cho trẻ em hình chữ nhật có chiều dài 100m và chiều rộng là 60m người ta làm một con đường nằm trong sân (hình vẽ). Biết rằng viền ngoài và viền trong của con đường là hai hình elip. Elip của đường viền ngoài có trục lớn và trục bé lần lượt song song với các cạnh của hình chữ nhật và chiều rộng của mặt đường là 2m. Kinh phí cho mỗi $m^{2}$ làm đường là 600.000 đồng. Tính tổng số tiền làm con đường đó (số tiền làm tròn đến hàng nghìn).
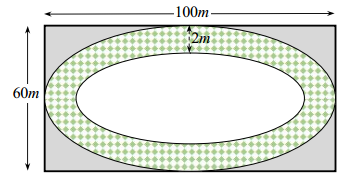
| A. 293904000 | B. 283904000 | C. 293804000 | D. 283604000 |
Giải: Đáp án A
Xét hệ trục tọa độ 0xy đặt gốc tọa độ 0 vào tâm của hình Elip.
Phương trình Elip của đường viền ngoài của con đường là $(E_{1}): \frac{x^{2}}{50^{2}}+\frac{y^{2}}{30^{2}}=1$. Phần đồ thị của $(E_{1})$ nằm bên trên trục hoành có phương trình $y=30 \sqrt{1-\frac{x^{2}}{50^{2}}}=f_{1}(x).$
Phương trình Elip của đường viền trong của con đường có phương trình $(E_{2}): \frac{x^{2}}{48^{2}}+\frac{y^{2}}{28^{2}}=1$. Phần đồ thị của $(E_{1})$ nằm bên trên trục hoành có phương trình $y=28 \sqrt{1-\frac{x^{2}}{48^{2}}}=f_{2}(x).$
$S=2(\int _{-50}^{50} 30 \sqrt{1-\frac{x^{2}}{50^{2}}} dx-\int _{-48}^{48} 28 \sqrt{1-\frac{x^{2}}{48^{2}}} dx)$.
Tính tích phân $I=2 \int _{-a}^{a} b \sqrt{1-\frac{x^{2}}{a^{2}}} dx, (a, b \in \mathbb{R}^{+})$.
Đặt $x=a \sin t\Rightarrow dx = a \cos t dt$.
Khi đó $I=2 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} b\sqrt{1-\sin^{2}t}a. \cos tdt=ab\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}(1+\cos 2t) dt=ab \pi$.
Do đó $S=50.30. \pi-48.28. \pi=156 \pi$.
Vậy tổng số tiền làm con đường là $600000. S \approx 294053000$ (đồng).
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận