Lời giải bài số 1, 4, 41, 48 Đề thi thử THPT quốc gia môn toán năm 2017 của trường THPT chuyên- ĐH Vinh lần 3
HƯỚNG DẪN GIẢI MỘT SỐ BÀI
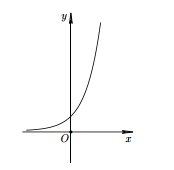 Câu 1: Cho hàm số $y=f(x)$ có đồ thị như hình bên. Biết rằng $f(x)$ là một trong bốn hàm số được đưa ra trong các phương án A, B, C, D dưới đây. Tìm $f(x)$.
Câu 1: Cho hàm số $y=f(x)$ có đồ thị như hình bên. Biết rằng $f(x)$ là một trong bốn hàm số được đưa ra trong các phương án A, B, C, D dưới đây. Tìm $f(x)$.
| A. $f(x)=e^{x}$ | B. $f(x)=(\frac{3}{\Pi})^{x}$ |
| C. $f(x)=\ln x$ | D. $f(x)=x^{\frac{e}{\Pi}}$ |
Giải: Đáp án A
Hàm số thuộc đồ thị trên luôn đồng biến trên $\mathbb{R}$ .
Loại B do $(\frac{3}{\Pi})<1$ nên hàm số $f(x)=(\frac{3}{\Pi})^{x}$ nghịch biến trên $\mathbb{R}$
Loại C, D do hàm số $f(x)=\ln x$ và $f(x)=x^{\frac{e}{\Pi}}$ không luôn đồng biến trên $\mathbb{R}$.
Câu 4: Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây là đúng?
A. Hàm số có hai điểm cực trị.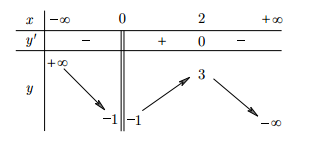
B. Hàm số nghịch biến trên mỗi khoảng xác định.
C. Hàm số có một điểm cực trị.
D. Giá trị lớn nhất của hàm số là 3.
Giải: Đáp án C
Tại khi $x=0$ đồ thị hàm số có đổi chiều nhưng $x=0$ không thỏa mãn điều kiện xác định nên loại A
Điểm $x=2, y=3$ là điểm cực đại nhưng $y=3$ không là giá trị lớn nhất của hàm số trên.
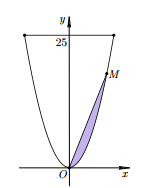 Câu 41: Ông B có một khu vườn giới hạn bởi một đường parabol và một đường thẳng. Nếu đặt trong hệ tọa độ 0xy như hình vẽ bên thì parabol có phương trình $y=x^{2}$ và đường thẳng y=25. Ông dự định dùng một mảnh vườn nhỏ được chia từ khu vườn bởi một đường thẳng đi qua 0 và một điểm m trên parabol để trồng một loại hoa. Hãy giúp ông xác định điểm M bằng cách tính độ dài 0M để diện tích mảnh vườn nhỏ bằng $\frac{9}{2}$.
Câu 41: Ông B có một khu vườn giới hạn bởi một đường parabol và một đường thẳng. Nếu đặt trong hệ tọa độ 0xy như hình vẽ bên thì parabol có phương trình $y=x^{2}$ và đường thẳng y=25. Ông dự định dùng một mảnh vườn nhỏ được chia từ khu vườn bởi một đường thẳng đi qua 0 và một điểm m trên parabol để trồng một loại hoa. Hãy giúp ông xác định điểm M bằng cách tính độ dài 0M để diện tích mảnh vườn nhỏ bằng $\frac{9}{2}$.
| A.$ OM=2 \sqrt{5}$ | C. $OM=10$ |
| B. $OM=15$ | D. $OM= 3 \sqrt{10}$ |
Giải: Đáp án D
Giả sử $M(a,a^{2})$ suy ra phương trình của OM là $y=ax$.
Khi đó diện tích khu vườn là $S=\int_{0}^{a}(ax-x^{2})dx=\frac{a^{3}}{6}=\frac{9}{2}\Leftrightarrow a=3$. Vậy $OM=3 \sqrt{10}$.
Câu 48: Cho tứ diện ABCD có AB=4a, CD=6a, các cạnh còn lại đều bằng $a \sqrt{22}$. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD.
| A. $\frac{5a}{2}$ | B. 3a | C. $\frac{a\sqrt{85}}{3}$ | D. $\frac{a\sqrt{79}}{3}$ |
Giải: Đáp án C
Gọi M, N là trung điểm của AB,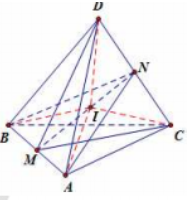 CD. Dễ dàng chứng minh được (DMC) và (ANB) lần lượt là mặt phẳng trung trực của đoạn thẳng AB và CD. Do đó tâm mặt cầu ngoại tiếp tứ diện ABCD là I nằm trên đường thẳng MN.
CD. Dễ dàng chứng minh được (DMC) và (ANB) lần lượt là mặt phẳng trung trực của đoạn thẳng AB và CD. Do đó tâm mặt cầu ngoại tiếp tứ diện ABCD là I nằm trên đường thẳng MN.
$MN= \sqrt{DM^{2}-DN^{2}}=\sqrt{DB^{2}-BM^{2}-DN^{2}}=3a$
Đặt $MI=x>0$. Ta có $\left\{\begin{matrix} BI^{2}=AI^{2}=BM^{2}+BI^{2}=4a^{2}+x^{2}\\DI^{2}=CI^{2}= DN^{2}+ IN^{2}= 9a^{2}+(3a \pm x)^{2}\\ \end{matrix}\right.$
$\Leftrightarrow 4a^{2}+x^{2}=9a^{2}+(3a \pm x)^{2} \Leftrightarrow x=\frac{7a}{3}\Rightarrow R=\frac{\sqrt{85}a}{3}$
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận