Giải Hoạt động khám phá trang 55 sgk Toán 8 tập 2 Chân trời
1. Tính chất đường phân giác của tam giác
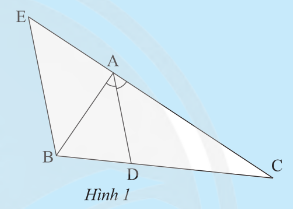
Hoạt động khám phá trang 55 sgk Toán 8 tập 2 CTST: Cho tam giác ABC có đường phân giác AD. Vẽ đường thẳng qua B song song với AD và cắt đường thẳng AC tại E (Hình 1). Hãy giải thích tại sao:
a) tam giác BAE cân tại A
b) $\frac{DB}{DC}=\frac{AE}{AC}=\frac{AB}{AC}$
a) Ta có: BE // AD suy ra $\widehat{AEB}=\widehat{CAD}$ (hai góc đồng vị), $\widehat{ABE}=\widehat{BAD}$ (hai góc so le trong)
AD là tia phân giác góc $\widehat{BAC}$ nên $\widehat{BAD}=\widehat{CAD}$
Do đó: $\widehat{AEB}=\widehat{ABE}$ suy ra tam giác BAE cân tại A
b) Xét tam giác BCE có AD // BE, theo định lí Thales ta có:
$\frac{DB}{DC}=\frac{AE}{AC}$
Mà AE = AB (do tam giác ABE cân tại A)
Do đó: $\frac{DB}{DC}=\frac{AE}{AC}=\frac{AB}{AC}$
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận