Giải Bài tập 3 trang 57 sgk Toán 8 tập 2 Chân trời

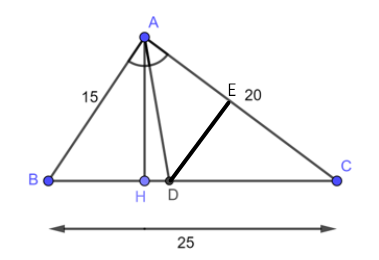
a) Trong tam giác ABC, ta có: AD là đường phân giác góc BAC

Suy ra: $\frac{DB}{DC}=\frac{AB}{AC}$ (tính chất đường phân giác)

Mà AB = 15 (cm); AC = 20 (cm)

Nên $\frac{DB}{DC}=\frac{15}{20}$

Suy ra: $\frac{DB}{DB +DC}=\frac{15}{15+20}$ (tính chất tỉ lệ thức)

Suy ra: $\frac{DB}{BC}=\frac{15}{35}$

Nên: $DB=\frac{15}{35}$ x 25 = $\frac{75}{7}$ cm

Do đó, $DC = BC-BD=25-\frac{75}{7}=\frac{100}{7}$ (cm)

Xét tam giác ABC có DE // AB, theo hệ quả định lí Thales ta có:

$\frac{DE}{AB}=\frac{CD}{BC}$ suy ra $\frac{DE}{15}=\frac{\frac{100}{7}}{25}$, vậy DE = $\frac{60}{7}$ cm

b) Xét tam giác ABC ta có: AB = 15 cm, AC = 20 cm, BC = 25 cm, nên $BC^{2}=AB^{2}+AC^{2}$ suy ra tam giác ABC vuông tại A

$S_{ABC}=\frac{1}{2}AC\times AB=\frac{1}{2}\times 20\times 15=150(cm^{2})$

c) Kẻ $AH\perp BC$ ta có:

$\frac{S_{ADB}}{S_{ABC}}=\frac{\frac{1}{2}AH\times BD}{\frac{1}{2}AH\times BC}=\frac{BD}{BC}=\frac{\frac{75}{7}}{25}=\frac{3}{7}$

Suy ra $S_{ADB}=\frac{3}{7}\times S_{ABC}=\frac{3}{7}\times 150=\frac{450}{7}(cm^{2})$

$\frac{S_{DCE}}{S_{ABC}}=\frac{\frac{1}{2}CE\times DE}{\frac{1}{2}AC\times AB}=(\frac{DE}{AB})^{2}=(\frac{\frac{60}{7}}{25})^{2}=\frac{144}{1225}$

Suy ra $S_{DCE}=\frac{144}{1225}\times S_{ABC}=\frac{144}{1225}\times 150=\frac{864}{49}(cm^{2})$

$S_{ADE}=S_{ABC}-S_{ADB}-S_{DCE}=150-\frac{450}{7}-\frac{864}{49}=\frac{3336}{49}(cm^{2})$