Giải Bài tập 4 trang 57 sgk Toán 8 tập 2 Chân trời

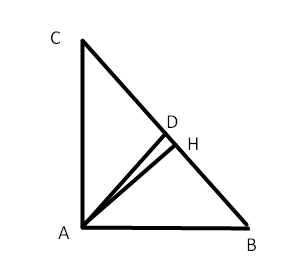
a) Tam giác ABC vuông tại A, áp dụng định lí Pythagore ta có: $BC^{2}=AC^{2}+AB^{2}$ suy ra BC = 5 cm

AD là tia phân giác góc A nên $\frac{DB}{DC}=\frac{AB}{AC}$ suy ra $\frac{DB}{5-DB}=\frac{3}{4}$

$\Rightarrow 4DB=15-3DB\Rightarrow DB=\frac{15}{7}$ (cm), do đó $DC=BC-DB=5-\frac{15}{7}=\frac{20}{7}$ (cm)

b) Ta có: $S_{ABC}=\frac{1}{2}AB\times AC=\frac{1}{2}AH\times BC$

$\Rightarrow AH=\frac{AB\times AC}{BC}=\frac{3\times 4}{5}=\frac{12}{5}$ (cm)

Tam giác ABH vuông tại H nên $HB=\sqrt{AB^{2}-AH^{2}}=\sqrt{3^{2}-(\frac{12}{5})^{2}}=\frac{9}{5}$ (cm)

Ta có: $HD=DB-HB=\frac{15}{7}-\frac{9}{5}=\frac{12}{35}$ (cm)

Tam giác ADH vuông tại H nên $AD=\sqrt{HD^{2}+AH^{2}}=\sqrt{(\frac{12}{35})^{2}+(\frac{12}{5})^{2}}=\frac{12\sqrt{2}}{7}$ (cm)