Giải hoạt động 7 trang 53 Chuyên đề toán 10 cánh diều
V. Đường chuẩn của Hypebol
Hoạt động 7. Cho hypebol (H) có phương trình chính tắc $\frac{x^{2}}{a^{2}}-\frac{b^{2}}{y^{2}}=1$ với a > 0, b > 0. Xét đường thẳng $\Delta 1: x=-\frac{a}{e}$
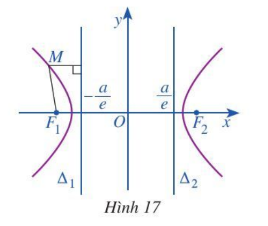
Với mỗi điểm M (x0; y0) ∈ (H) (Hình 17), tính:
a) Khoảng cách d (M, Δ1) từ điểm M(x0; y0) đến đường thẳng Δ1.
b) Tỉ số $\frac{MF1}{d(M,\Delta 1}$
a) Ta viết lại phương trình đường thẳng Δ1 ở dạng Δ1: $x + 0 \times y + \frac{a}{e} = 0.$
Với mỗi điểm M(x0; y0) thuộc hypebol, ta có:
$d(M,\Delta 1)=\frac{|x0+0\times y0+\frac{a}{e}|}{\sqrt{1^{2}+0^{2}}}=\frac{|a+ex0|}{e}=\frac{MF1}{e}$.
b) Từ a) ta suy ra $\frac{MF1}{d(M,\Delta 1}=e$
Xem toàn bộ: Giải chuyên đề toán 10 cánh diều bài 2 Hypebol
Giải những bài tập khác
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận