Giải câu 5 bài tích của một số với một vectơ
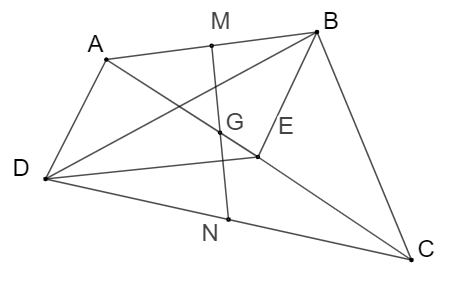
Bài tập 5. Cho tứ giác $A B C D$ có $M, N$ lần lượt là trung điểm của hai cạnh $A B$ và $C D$. Gọi $G$ là trung điểm của đoạn thẳng $M N, E$ là trọng tâm tam giác $B C D$. Chứng minh:
a. $\overrightarrow{E A}+\overrightarrow{E B}+\overrightarrow{E C}+\overrightarrow{E D}=4 \overrightarrow{E G}$;
b. $\overrightarrow{E A}=4 \overrightarrow{E G}$;
c. Điểm $G$ thuộc đoạn thẳng $A E$ và $\overrightarrow{A G}=\frac{3}{4} \overrightarrow{A E}$.
a. $\overrightarrow{E A}+\overrightarrow{E B}+\overrightarrow{E C}+\overrightarrow{E D}$
$=\overrightarrow{EM}+\overrightarrow{MA}+\overrightarrow{EM}+\overrightarrow{MB}+\overrightarrow{EN}+\overrightarrow{NC}+\overrightarrow{EN}+\overrightarrow{ND}$
$=2(\overrightarrow{EM}+\overrightarrow{EN})$
$=2(\overrightarrow{EG}+\overrightarrow{GM}+\overrightarrow{EG}+\overrightarrow{GN})$
$=4\overrightarrow{E G}$ (Đpcm)
b. E là trọng tâm tam giác $B C D$ $\Rightarrow \overrightarrow{E B}+\overrightarrow{E C}+\overrightarrow{E D}=\vec{0}$
$\Rightarrow \overrightarrow{E A}=4 \overrightarrow{E G}$
c. Vì $\overrightarrow{E A}=4 \overrightarrow{E G}$ $\Rightarrow G$ thuộc đoạn thẳng $A E$
Mặt khác: $\overrightarrow{E A}=4 \overrightarrow{E G} \Rightarrow \overrightarrow{AE}=4 \overrightarrow{GE} \Rightarrow \overrightarrow{GE} = \frac{1}{4} \overrightarrow{A E}$
$\Rightarrow \overrightarrow{A G}=\frac{3}{4} \overrightarrow{A E}$
Xem toàn bộ: Giải bài 5 Tích của một số với một vectơ

Bình luận